Question

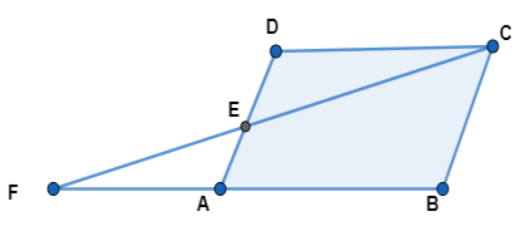
The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meet BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm. Then the perimeter of the parallelogram ABCD is

(a) 48 cm
(b) 44 cm
(c) 60 cm
(d) 50 cm
(e) 45 cm
(f) 54 cm
(d) None of the above

Answer 1

Hint: From the given figure, we will take two triangles $\left( \Delta DEC \right)$ and $\left( \Delta AEF \right)$. After then we will make the two triangles similar by $\left( AA \right)$ criterion for similarity. From that, we will take the ratio of each of the sides of the two triangles $\left( \Delta DEC \right)$ and $\left( \Delta AEF \right)$. By using the ratio we will find each of the sides of that parallelogram $\left( ABCD \right)$ and from the values of each side we can easily find the perimeter of the parallelogram.

Complete step-by-step answer:

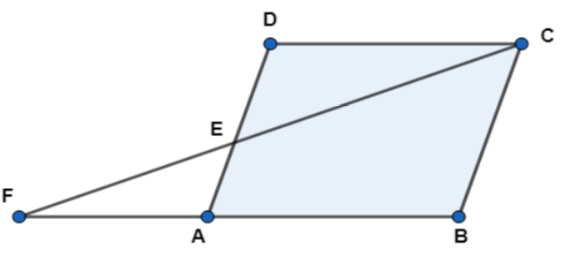
Let us consider a parallelogram $\left( ABCD \right)$, where E is a point in the side AD and CE is further produced to meet BA produced at point F.
It is also given in the question that side AE = 4 cm and side AF = 8 cm and another side AB = 12 cm.
Now we will consider two triangles $\left( \Delta DEC \right)$ and $\left( \Delta AEF \right)$. From these two triangles see that
$\angle DEC=\angle AEF$ (Vertically opposite angles)
Also $\angle EDC=\angle EAF$ (Alternate angles)
Therefore the two triangles $\left( \Delta DEC \right)$ and $\left( \Delta AEF \right)$ will be similar by the $\left( AA \right)$ of similarity.
As the two triangles $\left( \Delta DEC \right)$ and $\left( \Delta AEF \right)$ are similar, we will take the ratio of each sides of the two triangles i.e.
$\dfrac{DE}{AE}=\dfrac{EC}{EF}=\dfrac{DC}{AF}$
From the above we will take only two ratios
$\begin{align}
  & \Rightarrow \dfrac{DE}{AE}=\dfrac{DC}{AF} \\
 & \Rightarrow \dfrac{DE}{4}=\dfrac{12}{8} \\
\end{align}$
In the above we have substituted the value AE = 4 cm and AF = 8 cm which have already been given in the question.
$\begin{align}
  & \Rightarrow DE=\dfrac{12\times 4}{8} \\
 & \Rightarrow DE=6cm \\
\end{align}$
Now we will substitute the value of DE to find the value for AD
$\begin{align}
  & \Rightarrow AD=AE+DE \\
 & \Rightarrow AD=4+6 \\
 & \Rightarrow AD=10cm \\
\end{align}$
As we have found out all the sides of the parallelogram ABCD. Therefore the perimeter of the parallelogram ABCD
$\begin{align}
  & =AB+BC+CD+AD \\
 & =12+10+12+10 \\
 & =44cm \\
\end{align}$
Hence the perimeter of the parallelogram ABCD is 44 cm.

Note: Here in the above question similarity of triangles being used. This theorem plays a major role in finding each side of the two triangles, by which we can easily find the area as well as perimeter of triangles. Two triangles are said to be similar only when the following criterion follows:
(a) $AA\left( angle-angle \right)$
(b) $SSS\left( side-side-side \right)$
(c) $SAS\left( side-angle-side \right)$
(d) $ASA\left( angle-side-angle \right)$
That means all of if any two sides are equal, if all the sides are equal, if two sides and one angle are equal, or if two angles and one side are equal for any two triangles.
The above question can also be solved by taking the two triangles such as $\left( \Delta AFE \right)$and$\left( \Delta BFC \right)$. For this we also use the same method.