Question

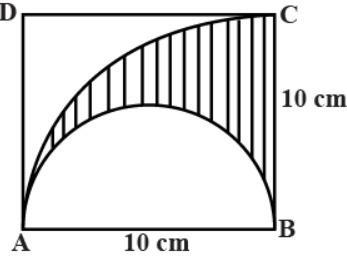
The given figure consists of a square, a quarter circle and a semicircle. Area of a sector is $\pi {r^2} \times \dfrac{\theta }{{{{360}^0}}}$. All the sides of a square are equal. Find the area of the shaded portion.

A. $\dfrac{{25}}{2}$sq. units
B. $25\pi $sq. units
C. $\dfrac{{25\pi }}{2}$sq. units
D. $\dfrac{{25\pi }}{4}$sq. units

Answer 1

Hint: In the given figure, we have been given a square, a quarter circle and a semicircle. To find the area of the shaded region, we will subtract the area of the semicircle from the area of the quarter circle. Quarter of the circle means the fourth part of the circle. To find the area of a quarter circle, we need the angle of the subtended. According to the figure, the side of the square is the diameter of a semicircle.

Complete step-by-step answer:
Step 1: Given side of the square $\left( {ABCD} \right) = 10$cm
It means $AB = BC = CD = DA = 10$cm because all the sides of the square are equal.
Diameter of semicircle (A to B) is equal to the side of square $AB$, that is diameter of semicircle $ = 10$cm
Radius of semicircle $\left( r \right) = \dfrac{{diameter}}{2}$
$ = \dfrac{{10}}{2}$
$ = 5$cm
Area of semicircle (A to B) $ = \dfrac{{\pi {r^2}}}{2}$ that is $\dfrac{{\pi \times {{\left( {radius} \right)}^2}}}{2}$
After solving \[ = \dfrac{\pi }{2} \times 5 \times 5\]
$ = \dfrac{{25\pi }}{2}c{m^2}$
We get the area of semicircle, that is $\dfrac{{25\pi }}{2}c{m^2}$
Step2: Angle of quarter circle $\left( \theta \right) = \dfrac{{{{360}^ \circ }}}{4}$
$ = {90^ \circ }$
Radius of quarter circle $\left( {BAC} \right) = BC = AB = 10$cm
Area of quarter circle $\left( {BAC} \right) = \dfrac{\theta }{{360}} \times \pi {r^2}$
After solving,
$ = \dfrac{{90}}{{360}} \times \pi \times 10 \times 10$
$ = 25\pi c{m^2}$
We get the area of quarter circle $\left( {BAC} \right)$, that is $25\pi c{m^2}$
Step 3: To find the area of shaded region, we subtract the area of semicircle (A to B), from the area of quarter circle $\left( {BAC} \right)$, that is
Area of shaded region $ = $ area of quarter circle $\left( {BAC} \right) - $ area of semicircle (A to B)
$ \Rightarrow 25\pi - \dfrac{{25\pi }}{2}$
After solving we get,
$ = \dfrac{{25\pi }}{2}c{m^2}$
So, the area of the shaded region is $\dfrac{{25\pi }}{2}c{m^{}}$square units.

Hence, option C is correct.

Note: So far, we calculated the areas of different figures separately. We calculated the areas of some combinations of plane figures. We came across these types of figures in our daily life and also in the form of various interesting designs. Circle is a shape consisting of all points in a plane that are fixed distance from the given point.