Question

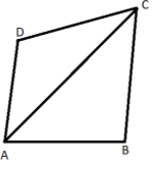
The given fig is drawn using more than one triangle: \[\angle DAB + \angle ABC + \angle BCD + \angle CDA\]

Answer 1

Hint: Here we will use the property of the triangle for the sum of the angles. Then we will write the equation for the sum of the angles of both the triangles and then we will add all the angles. Then we will simplify the equation further to get the required value.

Complete step-by-step answer:
It is given that the given figure is drawn by using the triangles and we can see that there are two triangles used to make the figure.
So, we will use the basic property of the triangle i.e. sum of all the angles of a triangle is equal to \[180^\circ \]. Therefore, we will write the equation for all the angles of the two triangle.
For triangle \[\Delta ABC\]
\[\angle ABC + \angle BCA + \angle CAB = 180^\circ \]……………………….. \[\left( 1 \right)\]
For triangle \[\Delta ACD\]
\[\angle ACD + \angle CDA + \angle DAC = 180^\circ \]……………………….. \[\left( 2 \right)\]
Now we will add both the equation \[\left( 1 \right)\] and equation \[\left( 2 \right)\]. Therefore, we get
\[\angle ABC + \angle BCA + \angle CAB + \angle ACD + \angle CDA + \angle DAC = 180^\circ + 180^\circ \]
We can write the above equation as
\[ \Rightarrow \angle ABC + \left( {\angle BCA + \angle ACD} \right) + \left( {\angle CAB + \angle DAC} \right) + \angle CDA = 180^\circ + 180^\circ \]
We know that the sum of the angle \[\angle BCA\] and angle \[\angle ACD\] is equal to \[\angle BCD\]. Also the sum of the angle \[\angle CAB\] and angle \[\angle DAC\] equal to angle \[\angle DAB\]. Therefore, we get
\[ \Rightarrow \angle ABC + \left( {\angle BCD} \right) + \left( {\angle DAB} \right) + \angle CDA = 360^\circ \]
\[ \Rightarrow \angle DAB + \angle ABC + \angle BCD + \angle CDA = 360^\circ \]
Hence the value of \[\angle DAB + \angle ABC + \angle BCD + \angle CDA\] is equal to \[360^\circ \].

Note: We can also solve this by using the basic property of the quadrilateral which states that the sum of all the interior angles of a quadrilateral shape is equal to \[360^\circ \]. We will use this property also because the figure drawn using the triangles forms a quadrilateral shape. Quadrilateral is a shape which consists of four sides whereas triangle is a polygon with three edges or sides and three vertices. Side is one of the straight line segments which are used to construct or draw a polygon.