Question

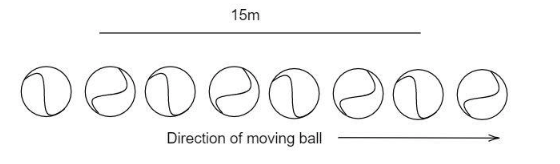
The given diagram shows a series of images of moving balls captured by a camera. The ball was moving at a constant speed and the images were taken at a constant rate of $10$ per second. What is the speed of the ball?

(A) $30\,m{s^{ - 1}}$
(B) $20\,m{s^{ - 1}}$
(C) $45\,m{s^{ - 1}}$
(D) $15\,m{s^{ - 1}}$

Answer 1

Hint:From the given diagram, calculate the distance covered by the ball at a single image taken. Substitute the value of the distance covered and the time taken in the formula of the speed of the ball to obtain the value of the speed. This gives the rate at which the ball moves at a time of taking photographs.

Formula used:
The speed of the ball is given by
$s = \dfrac{d}{t}$
Where $s$ is the speed of the ball that moves, $d$ is the distance covered by the ball and $t$ is the time taken by the ball to cover that distance.

Complete step by step solution:
It is given that the
Rate at which the image of the ball movement taken, $r = 10\,{s^{ - 1}}$.
From the diagram, it is clear that the ball covers $5$ position in $15$ distance. Hence the distance covered by the ball for its single position is calculated as follows.
$5x = 15$
In the above step, the $x$ means the ball position. By simplifying the above step.
$x = 3\,m$
Substitute the value of the calculated distance and the time taken in the formula of the speed of the ball.
$s = \dfrac{d}{t}$
It is given that the image was taken $10\,{s^{ - 1}}$ . So the time taken is $\dfrac{1}{{10}}\,s$ .
$s = \dfrac{3}{{\dfrac{1}{{10}}}}$
By the simplification of the above step,
$s = 30\,m{s^{ - 1}}$

Hence the speed of the ball is calculated as $30\,m{s^{ - 1}}$ .

Note:The speed of the ball is directly proportional to its distance and it is inversely proportional to the time taken to cover the distance. The time taken to take the image and the time taken for the ball movement is considered the same, since both take place simultaneously.