Question

The function p(x) has four distinct roots, which of the following graphs can represent p(x)?

A)

B)

C)

D)

Answer 1

Hint:
Here we have to find the curve which is showing the 4 roots of the function \[p\left( x \right)\]. If a function is represented on the graph then at the distinct intersection of the curve with the \[x\]-axis will give us the distinct roots of the function. So, by using the same concept we will find the curve which intersects the \[x\]-axis 4 times for its 4 distinct roots.

Complete step by step solution:
It is given that the given function \[p\left( x \right)\] has four distinct roots which means when the function is plotted on the graph then the function curve will intersect four times at different points on the x-axis.
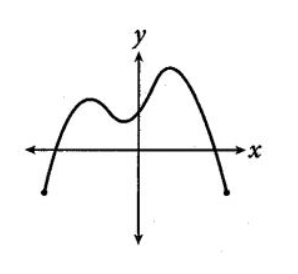
For the first option given, the curve of the function is only intersecting the \[x\]-axis two times. It means the curve of the function given has only 2 distinct roots. So, the curve in option A is not the curve of the required function.
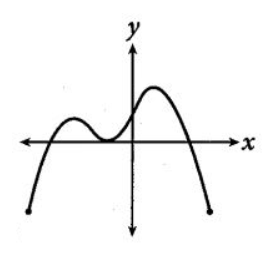
For the second option given, the curve of the function is only intersecting the \[x\]-axis three times which means the curve of the function given has only 3 distinct roots. So, the curve in option B is not the curve of required function.
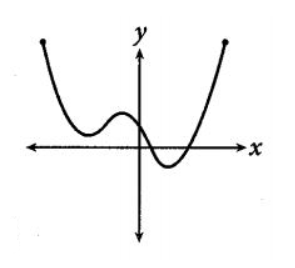
Now in the third option, the curve of the function intersects the \[x\]-axis two times which means the curve of the function given has only 2 distinct roots. So the curve in option C is not the curve of required function.
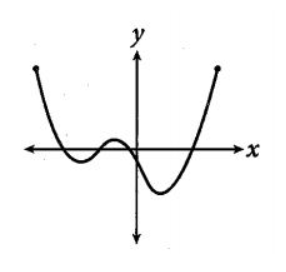
For the fourth option, the curve of the function is intersecting the \[x\]-axis four times at four different points which means the curve of the function given has 4 distinct roots so the curve in option D is the curve of required function.
Hence, the curve given in the option D is the curve of the function \[p\left( x \right)\] which has 4 distinct roots.

So, option D is correct.

Note:
Roots of a function are defined as the number or location at which the value of the function is always zero then that number or location is known as the roots of the function. We need to remember that whenever we plot a curve of a function on the graph then its intersection on the \[x\]-axis is the root of the function at which the value of \[y\] is equal to zero always and at each point of intersection the function has a distinct root. A function can have more than one root. A function can be represented in terms of curves on the graph i.e. any function can be plotted on the graph with the help of their variables.