Question

The friction of air causes vertical retardation equal to \[10\% \]of the acceleration due to gravity (Take\[g = {10^{{\text{ m se}}{{\text{c}}^{ - 2}}}}\]). The maximum height will be decreased by
A. \[8\% \]
B. \[9\% \]
C. \[10\% \]
D. \[11\% \]

Answer 1

Hint: When an object is thrown in the air it reaches a height and then fall back, but when the object is thrown in the air where there is friction in the air then the ball will not gain the same height its trajectory will be short.
In this question find the ratio of maximum height reached by an object without air friction to the maximum height reached by the object when there is friction in the air.

Complete step by step answer:
Retardation\[ = 10\% \]

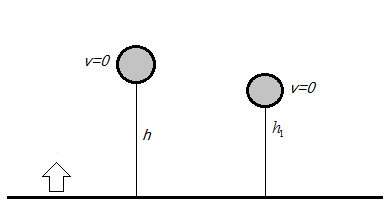
When an object reaches its maximum height, then the objects stop moving up, and then it tends to fall down hence we can say at a maximum height which will be the final velocity point of an object, the velocity is \[v = 0\].
So the in the equation of the motion can be written as:
\[{v^2} = {u^2} + 2gh\]
As, \[v = 0\] so, the above equation can be re-written as:
\[
  {0^2} = {u^2} + 2gh \\
  h = \dfrac{{ - {u^2}}}{{2g}} \\
  h \propto \dfrac{-1}{g} - - - - (i) \\
 \]
Now when there is air resistance \[10\% \] of the gravity, new gravity will be
\[
  {g_{ef}} = g + 0.1g \\
   = 1.1g \\
   = \dfrac{{11g}}{{10}} \\
 \]
Hence the new maximum height reached will be given as:
\[
  {h_1} = \dfrac{{ - {u^2}}}{{2{g_{ef}}}} \\
  {h_1} \propto \dfrac{-1}{{{g_{ef}}}} - - - - (ii) \\
 \]
Since height reached by an object is inversely proportional to the gravity, hence we can write from the equations (i) and (ii) as:
\[\dfrac{{{h_1}}}{h} = \dfrac{g}{{{g_{ef}}}} - - - - (iii)\]
Equation (iii) can also be written as:
\[
  1 - \dfrac{{{h_1}}}{h} = 1 - \dfrac{g}{{{g_{ef}}}} \\
  \dfrac{{h - {h_1}}}{h} = \dfrac{{{g_{ef}} - g}}{{{g_{ef}}}} \\
  \dfrac{{\vartriangle h}}{h} = \dfrac{{\left( {\dfrac{{11}}{{10}}g} \right) - g}}{{\left( {\dfrac{{11}}{{10}}g} \right)}} \\
   = \dfrac{{\left( {\dfrac{1}{{10}}g} \right)}}{{\left( {\dfrac{{11}}{{10}}g} \right)}} \\
   = \dfrac{1}{{11}} \\
 \]
Therefore the percentage change in maximum height will be
\[
  \dfrac{{\vartriangle h}}{h} = \dfrac{1}{{11}} \times 100\% \\
   = 9.09\% \\
   \approx 9\% \\
 \]
Hence, the maximum height of the ball will be decreased by 9%.

So, the correct answer is “Option B”.

Note:
Students must note that whenever there is friction, then the natural trajectory of any object falls short as a backward force (resisting the forward motion) acts on the object.Also When an object reaches its maximum height, then the objects stop moving up, and then it tends to fall down