Question

The frequency of the characteristic X ray of ${{K}_{a}}$ line of metal target ‘M’ is $2500c{{m}^{-1}}$ and the graph between $\surd v$ vs ‘z’ is as follows, then the atomic number of M is?

Answer 1

Hint: The concept of Moseley’s Law is to be used in this question. Form an equation containing all the parameters of the Moseley’s Law and compare it with the equation of a straight line and find the unknown constants.

Complete step by step answer:
In order to answer our question, we need to know about the structure of atoms as well as the application of Moseley’s law. Moseley’s law tells us the characteristics when X rays get emitted out by the atoms. The law was introduced by Henry Moseley and the law states that the atomic number is directly proportional to the square root of the frequency of the emitted X ray. Mathematically, $\sqrt{v}\,\alpha \,Z$.
- It was found out that the ${{K}_{a}}$ lines had a relation with the atomic number. When it got incorporated with Bohr’s model, the new formula that started Moseley’s Law was:
\[\upsilon =A{{(Z-b)}^{2}}\]
- Here, $\upsilon $ is the frequency of the X-ray emission line and A and b are the constants which depend on the line type, like K, L, etc.
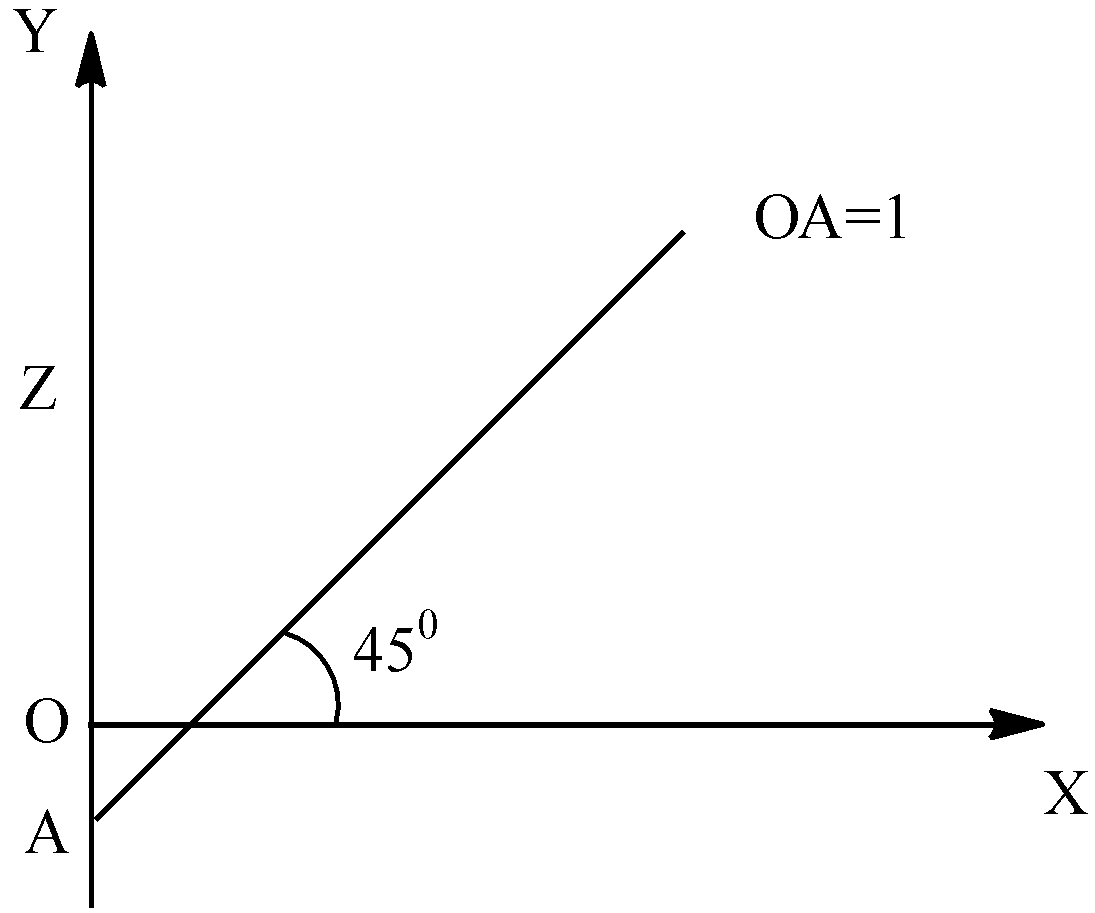
- Now, let us come to the solution. We have the graph and the frequency of the X Ray as $2500c{{m}^{-1}}$. Now, according to the Moseley’s Law, we can write:
\[\begin{align}
 & \sqrt{\upsilon }={{k}_{1}}(Z-{{k}_{2}}) \\
 & \Rightarrow \sqrt{\upsilon }={{k}_{1}}Z-{{k}_{1}}{{k}_{2}} \\
\end{align}\]
- On comparing this with the equation of a straight line that is, y=mx+c, we can relate the LHS and RHS as:
\[\begin{align}
 & y=\sqrt{\upsilon }=\sqrt{2500}=50 \\
 & x=z \\
 & m={{k}_{1}}=\tan \,{{45}^{0}}=1 \\
 & c=-{{k}_{1}}{{k}_{2}} \\
 & OA=1;-{{k}_{1}}{{k}_{2}}=1 \\
 & \Rightarrow {{k}_{2}}=-1 \\
\end{align}\]
- Now, let us use the above information in order to find the required atomic number.
\[\begin{align}
 & \sqrt{\upsilon }={{k}_{1}}Z-{{k}_{1}}{{k}_{2}} \\
 & \Rightarrow 50 = 1\times Z-(1)(-1) \\
 & \Rightarrow 50 = Z + 1 \\
 & \Rightarrow Z = 49 \\
\end{align}\]
So, we find the value of the atomic number as 49, which is the required answer for our question.

Note: For finding constants A and B we have $A = (\dfrac{1}{{{1}^{2}}}-\dfrac{1}{{{2}^{2}}})$ and b = 1 for the lines which fall in the ${{K}_{a}}$ series.