Question

The freezing point of benzene decreases by ${0.45^0}C$ when $0.2$ g acetic acid is added to $20$g of benzene. If acetic acid associates to form a dimer in benzene, percentage association of acetic acid in benzene will be:
[ ${K_f}$ for benzene $ = 5.12K - kg - mo{l^{ - 1}}$]
A. $74.6\% $
B. $94.6\% $
C. $64.6\% $
D. $80.4\% $

Answer 1

Hint: We can solve this problem with the formula of freezing point depression concept. Freezing point is the temperature at which the vapour pressure of both the liquid solvent and solid solvent are equal at equilibrium. The freezing point depression is also a colligative property of solution.

Complete step by step answer:
 If the freezing point of solvent decreases after addition of non-volatile solutes, it is called freezing point depression. Freezing point depression is also termed as “Cryoscopy”. It is denoted as \[\Delta {T_f}\] i.e. freezing point of pure solvent – freezing point of solution. Graph for freezing point depression can show below:

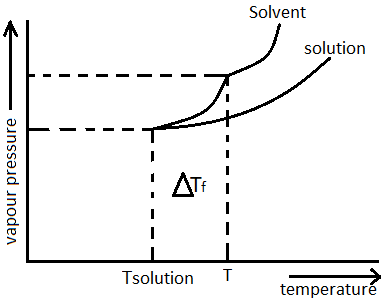
Mathematically it is represented as $\Delta {T_f} = {K_f}m$ , where $m$ is the molality of solution, ${K_f}$ is the cryoscopic constant or molal depression constant which depends only on the properties of the solvent, not the solute.
Hence the formula we used in this question is $\Delta {T_f} = {K_f}\dfrac{w}{M} \times \dfrac{{1000}}{W}$ where $M$is the molarity of solution, $w$is the weight of solute and $W$is the weight of solvent.
Van’t Hoff introduced a factor called van’t Hoff factor denoted as $'i'$ in all the formula of colligative property of solutions. It expresses the limits of dissociation and association of solutes in solution.
And the formula of degree of association is: $\alpha = \dfrac{{i - 1}}{{1/n - 1}}$ where $n$is the number of particles in the solution.
So, the modified formula of freezing point of depression, $\Delta {T_f} = i{K_f}m$.
In the question, it is given that the acetic acid associates to form a dimer in benzene hence, $n = 1/2$
$2C{H_3}COOH \rightleftharpoons {\left( {C{H_3}COOH} \right)_2}$ this reaction takes place in the benzene.
$i = 1 + (1/2 - 1)\alpha $$ \Rightarrow i = 1 - \dfrac{\alpha }{2}$
$\Delta {T_f} = 0.45,{K_f} = 5.12$ hence,
$\begin{gathered}
  0.45 = \left( {1 - \dfrac{\alpha }{2}} \right)\left( {5.12} \right)\dfrac{{0.2}}{{60}} \times \dfrac{{1000}}{{20}} \\
  1 - \dfrac{\alpha }{2} = 0.527 \\
  \alpha = 0.945 \\
\end{gathered} $
Then, percentage association of acetic acid in benzene will be: $94.5\% $
So, the correct answer is “Option B”.

Note: If the molality of solution is equal to one, then $\Delta {T_f} = {K_f}$. For the calculation of molal depression in freezing point$(K)$, we use $K = 10{K_f}$ in the above formula of $\Delta {T_f}$. Information about $\Delta {T_f}$ is useful for melting ice on the road and making antifreeze solutions.