Question

The four vertices of a quadrilateral are (1, 2), (-5, 6), (7, -4) and (k, -2) taken in order. If the area of the quadrilateral is zero, find the value of k.

Answer 1

Hint: In this particular question use the concept that the area of the quadrilateral is the sum of the area of the two triangles as shown in the above figure so calculate the area of each triangle and then add up, so use these concepts to reach the solution of the question.

Complete step-by-step answer:

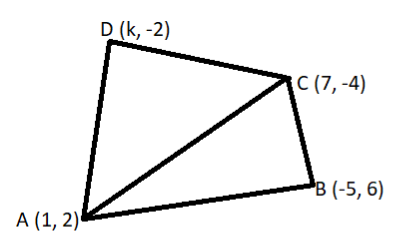
Let us consider the quadrilateral ABCD as shown above.
Let,
A = (${x_1},{y_1}$) = (1, 2)
B = (${x_2},{y_2}$) = (-5, 6)
C = (${x_3},{y_3}$) = (7, -4)
D = (${x_4},{y_4}$) = (k, -2)
So first calculate area of triangle ABC
So area of triangle ABC = $\dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  {{x_1}}&{{y_1}}&1 \\
  {{x_2}}&{{y_2}}&1 \\
  {{x_3}}&{{y_3}}&1
\end{array}} \right|$
Now substitute the values we have,
The area of triangle ABC = $\dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  1&2&1 \\
  { - 5}&6&1 \\
  7&{ - 4}&1
\end{array}} \right|$
Now expand the determinant we have,
$ \Rightarrow {A_1} = \dfrac{1}{2}\left[ {1\left| {\begin{array}{*{20}{c}}
  6&1 \\
  { - 4}&1
\end{array}} \right| - \left( 2 \right)\left| {\begin{array}{*{20}{c}}
  { - 5}&1 \\
  7&1
\end{array}} \right| + 1\left| {\begin{array}{*{20}{c}}
  { - 5}&6 \\
  7&{ - 4}
\end{array}} \right|} \right]$
Now simplify it we have,
$ \Rightarrow {A_1} = \dfrac{1}{2}\left[ {1\left( {6 - \left( { - 4} \right)} \right) - 2\left( { - 5 - 7} \right) + 1\left( {20 - 42} \right)} \right]$
$ \Rightarrow {A_1} = \dfrac{1}{2}\left[ {10 + 24 - 22} \right] = \dfrac{{12}}{2} = 6$ sq. units.
Now the area of the triangle ACD
So area of triangle ACD = $\dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  {{x_1}}&{{y_1}}&1 \\
  {{x_3}}&{{y_3}}&1 \\
  {{x_4}}&{{y_4}}&1
\end{array}} \right|$
Now substitute the values we have,
The area of triangle ABC = $\dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  1&2&1 \\
  7&{ - 4}&1 \\
  k&{ - 2}&1
\end{array}} \right|$
Now expand the determinant we have,
$ \Rightarrow {A_2} = \dfrac{1}{2}\left[ {1\left| {\begin{array}{*{20}{c}}
  { - 4}&1 \\
  { - 2}&1
\end{array}} \right| - \left( 2 \right)\left| {\begin{array}{*{20}{c}}
  7&1 \\
  k&1
\end{array}} \right| + 1\left| {\begin{array}{*{20}{c}}
  7&{ - 4} \\
  k&{ - 2}
\end{array}} \right|} \right]$
Now simplify it we have,
$ \Rightarrow {A_2} = \dfrac{1}{2}\left[ {1\left( { - 4 - \left( { - 2} \right)} \right) - 2\left( {7 - k} \right) + 1\left( { - 14 - \left( { - 4k} \right)} \right)} \right]$
$ \Rightarrow {A_2} = \dfrac{1}{2}\left[ { - 2 - 14 + 2k - 14 + 4k} \right] = \dfrac{{ - 30 + 6k}}{2} = - 15 + 3k$ sq. units.
Now the total area (A) of the quadrilateral is the sum of the above calculated areas.
$ \Rightarrow A = {A_1} + {A_2}$
$ \Rightarrow A = 6 + \left( { - 15 + 3k} \right)$
Now it is given that the area of the quadrilateral is zero.
So equate the above equation to zero we have,
$ \Rightarrow A = 6 + \left( { - 15 + 3k} \right) = 0$
$ \Rightarrow 6 - 15 + 3k = 0$
$ \Rightarrow 3k = 9$
$ \Rightarrow k = 3$
So this is the required value of k.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall the formula of the area of the triangle in determinant format which is stated above, so just substitute the values in the formula as above we will get the required answer.