Question

The formula of total surface area of a cone is__________.

Answer 1

Hint: In this question we derive the formula for Total Surface Area . For this we need to find the Curved Surface Area of Cone and the base area of the cone which looks like a circle. For finding Curved Surface Area we need to open the curved top and cut into pieces of triangles.
The surface area of a cone is equal to the curved surface area plus the area of the base. The curved surface area is also known as lateral surface area.

Complete step-by-step answer:
Consider a cone of $ r $ radius , $ h $ height and $ l $ slant height. Slant height is the height of a cone from the vertex to the periphery (rather than the centre) of the base.

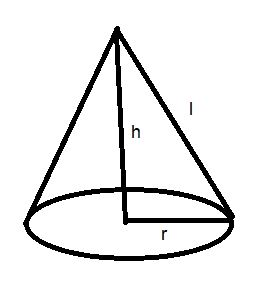
Surface Area of a Cone = Curved Surface Area of Cone + Base Area of Cone ----eq.1
Since, the Base Area of cones is in circular shape. So, Base Area of cone = $ \pi {r^2} $ -----eq.2
Now, the Curved Surface Area of Cone: Now if open the curved top and cut into small pieces, so that each cut portion is a small triangle, whose height is the slant height $ l $ of the cone.

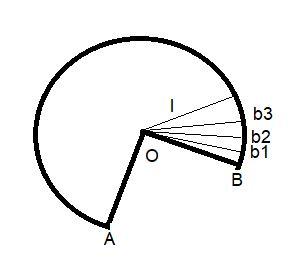
Now the area of each triangle = $ \dfrac{1}{2}({\text{base of each triangle}} \times l) $
∴ Area of the curved surface = sum of the areas of all the triangles
     $
   = \dfrac{1}{2} \times {b_1} \times l + \dfrac{1}{2} \times {b_2} \times l + ............ + \dfrac{1}{2} \times {b_n} \times l \\
   = \dfrac{1}{2} \times l \times ({b_1} + {b_2} + ........... + {b_n}) \\
   = \dfrac{1}{2} \times l \times ({\text{curved surface}}){\text{ ----- eq}}{\text{.3}} \\
$
From the figure, we know that the curved surface is equivalent to the perimeter of the base of the cone.
The circumference of the base of the cone = $ 2\pi r $
Then, Area of the curved surface \[ = \dfrac{1}{2} \times l \times ({\text{circumference of base circle}}){\text{ }}\]
 $
   \Rightarrow {\text{Area of curved surface area}} = \dfrac{1}{2} \times l \times (2\pi r) \\
   \Rightarrow {\text{Area of curved surface area}} = \pi lr{\text{ -----eq}}{\text{.4}} \\
    \\
  $
 Now, from eq.2 and eq.3 we can rewrite eq.1 as
 $
   \Rightarrow {\text{Surface Area of Cone = }}\pi rl{\text{ + }}\pi {r^2} \\
   \Rightarrow {\text{Surface Area of Cone = }}\pi r(l{\text{ + }}r){\text{ }}{{\text{ }}^{}} \\
 $
Hence, the Surface Area of Cone is $ \pi r(l + r) $ .

Note: - Whenever you get this type of problem the key concept of solving is to derive the formula for the same. For this you need to learn some basic formulas of different shapes, also the analysis of different shapes on cutting like in this question we need to cut the cone into pieces to get a small triangle .