Question

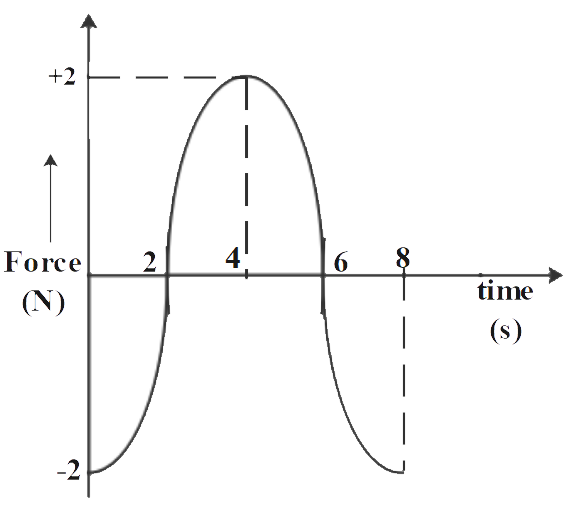
The force-time (F-t) curve of a particle executing linear motion is as shown in the figure. The momentum acquired by the particle in time interval of zero to 8 seconds will be (in Ns):

                

A. -2
B. 4
C. 6
D. 0

Answer 1

Hint: The area under the (F-t) curve and time axis will give us the momentum acquired by the particle. Momentum is a quantity of motion. Every moving object with mass has a momentum. The unit of momentum is Ns in the SI system. Momentum is calculated by taking the product of mass of the object and its velocity.

Formula used:
\[F=\dfrac{dp}{dt}\]

Complete answer:
So, to find the momentum from the given curve of Force-time we need to find the total area under the curve. For that, let us divide the area in three intervals like the figure i.e. (0-2) seconds, (2-6) seconds, (6-8) seconds.
 We know that force is the rate at which momentum is changed with respect to time.
Therefore,
 area under first interval of curve = \[-2\times 2=-4\]
area under second interval of curve = \[2\times (6-2)=8\]
area under third interval of curve = \[-2\times (8-6)=-4\]
Now, to find the total area under the curve.
Let us add the area for all three intervals
Therefore,
area under first interval of curve area under second interval of curve area under third interval of curve = \[\left( -4 \right)+8+\left( -4 \right)=0\]
The total area under the Force-time (F-t) curve is zero.

So, the correct answer is “Option D”.

Additional Information:
\[F=\dfrac{dp}{dt}\]
Now,
We know,
\[p=mv\]
The above formula gives us Newton’s third law and also conservation momentum
\[F=m\dfrac{dv}{dt}\]

Note:
This same question can be solved by using integration to find the area under the curve. However, this would consume a considerable amount of tie and students need to know the rules for integration.