Question

The force of gravitation is
(A) Repulsive
(B) Conservative
(C) Electrostatic
(D) Non-conservative

Answer 1

Hint :Observe different properties of gravitational force using the equation of gravitational force. The equation for gravitational force is given by, $ F = \dfrac{{GMm}}{{{R^2}}} $ . Where, $ m $ and $ M $ are the masses of two bodies separated by a distance $ R $

Complete Step By Step Answer:
We know that, the gravitational force acting on a body of mass $ M $ by a mass $ m $ or vice versa separated by a distance $ R $ is given by, $ \vec F = \dfrac{{GMm}}{{{R^2}}}\hat R $ . Where, $ G $ is the gravitational constant.
So, we can see that, $ F\alpha \dfrac{1}{{{R^2}}} $ If both the masses are constant. So, the direction of force is the direction of the relative position vector $ \vec R $ . So, the Force is a repulsive one.
Hence, option ( A) is correct.

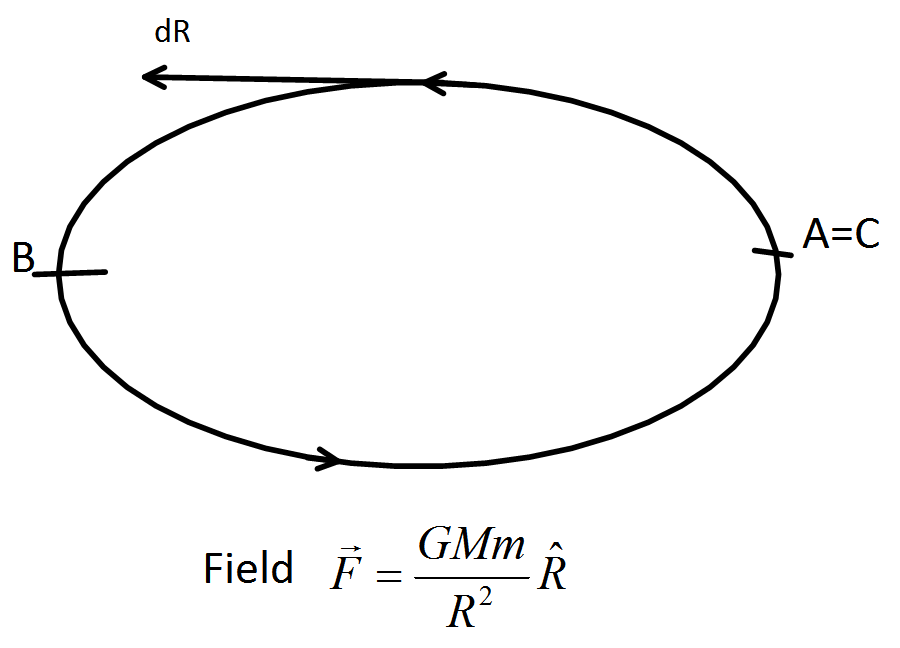
Now, we know, a force field is said to be conserved if the work done over a closed path is zero.
So, let a ABC is a closed path then, work done to take the mass $ M $ in a Gravitational force field $ \vec F = \dfrac{{GMm}}{{{R^2}}}\hat R $ from A to B is, $ W = \int\limits_A^B {F.dR} $
Putting the value of $ F $ we get,
 $ {W_1} = \int\limits_A^B {\dfrac{{GMm}}{{{R^2}}}dR} $
 $ GMm\left[ { - \dfrac{1}{R}} \right]_A^B $
 $ = GMm\left[ {\dfrac{1}{{{R_A}}} - \dfrac{1}{{{R_B}}}} \right] $
Now work done to take the mass $ M $ in a Gravitational force field $ \vec F = \dfrac{{GMm}}{{{R^2}}}\hat R $ from A to B is, $ W = \int\limits_B^{C = A} {F.dR} $
 $ {W_2} = \int\limits_B^A {\dfrac{{GMm}}{{{R^2}}}dR} $
 $ = GMm\left[ { - \dfrac{1}{R}} \right]_B^A $
 $ = GMm\left[ {\dfrac{1}{{{R_B}}} - \dfrac{1}{{{R_A}}}} \right] $
Net work done is ,
 $ {W_1} + {W_2} = GMm\left[ {\dfrac{1}{{{R_A}}} - \dfrac{1}{{{R_B}}}} \right] + GMm\left[ {\dfrac{1}{{{R_B}}} - \dfrac{1}{{{R_A}}}} \right] $
That becomes,
 $ = GMm\left[ {\dfrac{1}{{{R_A}}} - \dfrac{1}{{{R_B}}} + \dfrac{1}{{{R_B}}} - \dfrac{1}{{{R_A}}}} \right] $
 $ = 0 $
Hence, the gravitational force field is a conservative force field.
Hence, option ( B) is correct and option ( D) is incorrect.
We can see in gravitational force, there is no term for charges hence it cannot be an electrostatic force.
Hence, option ( C) is incorrect.
Hence, option (A) and (B) are correct choices.

Note :
Gravitational force can only be realizable only if one or both of the mass is very large or power of the term $ \dfrac{{Mm}}{{{R^2}}} $ is $ {10^{11}} $ since, $ G = 6.67 \times {10^{ - 11}}N{m^2}k{g^{ - 2}} $ . When the distance is very small (atomic level) gravitational force vanishes, then there are only atomic or nuclear forces.