Question

The force F on a particle moving in a straight line varies with distance d as shown in figure. The work done on the particle during its displacement of $12m$ is:

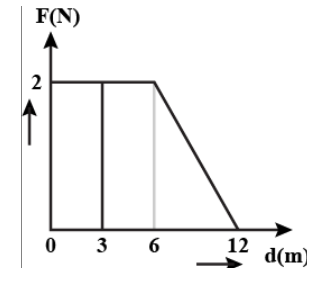
$\begin{align}
  & \text{A}\text{. 18J} \\
 & \text{B}\text{. 21J} \\
 & \text{C}\text{. 26J} \\
 & \text{D}\text{. 13J} \\
\end{align}$

Answer 1

Hint: The area under force and displacement graph will give the work done during the displacement. The total area is the area of the rectangle of length \[6\] and breadth\[2\], and the area of the right angle triangle of base length $6$and height\[2\]. After finding an area add them to get the work done.

Formulas used:
Area of rectangle of length $l$ and breadth $b$ is $A=lb\text{ sq units}$
Area of right-angled triangle with base length $b$ and height $h$ is $A=\dfrac{1}{2}bh\text{ sq units}$

Complete answer:

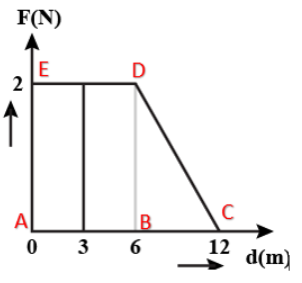
The area under the force and displacement curve will give the work done during the displacement.
So the area under the curve is the sum of area of rectangle $ABDE$ and area of right-angled triangle$BCD$
Area of rectangle $ABDE$ is ${{A}_{1}}=length\times breadth=6\times 2=12=12$
Area of triangle $BCD$is ${{A}_{2}}=\dfrac{1}{2}\times base\times height=\dfrac{1}{2}\times 6\times 2 = 6$
Total area $A={{A}_{1}}+{{A}_{2}}=12+6=18$
So the work done on the particle during its displacement of $12m$ is $18J$

So the correct option is $\text{A}\text{. 18J}$.

Note:
Just like this the graph between position-time, velocity-time, can be plotted and also the equation of motions can be derived from these graphs.
Taking position is taken in y-axis and the time is taken in x-axis then the graph of a stationary object will give a straight line parallel to time axis.
The position-time graph for an object with uniform motion will give a straight line and the slope of the graph will give the velocity of the particle.
The position-time graph for a uniformly accelerated motion is a parabola and the slope of this graph will give the instantaneous velocity at that instant.
If you take time in x-axis and the velocity in y-axis then the graph for a uniform motion will give a straight line parallel to the time axis. The area under the velocity-time curve will give displacement.
The velocity-time graph for a uniformly accelerated motion is a straight line and the slope will give the acceleration and the area under the line will give the displacement.