Question

The foot of a 20 ft. ladder is 12 ft. from the base of the house. How far up the side of the house does the ladder reach?

Answer 1

Hint: try to construct all the given information in the form of a figure. This will get you closer to the, as the figure will decide what kind of law or theorem can be used to solve the problem above. As this construction will turn into a right angle triangle, try using Pythagoras theorem to get the desired value.

Complete step-by-step answer:
It’s given in the question that the ladder is 20 ft. Also it is placed at a distance of 12 ft from the base of the house.
We will first try to construct a figure with the given information.

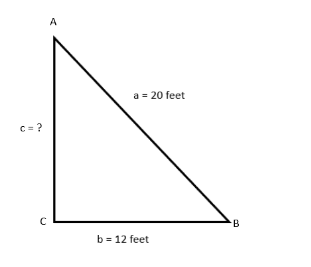
So let a be the length of the ladder $ \Rightarrow a = 20 $ feet
Let b be the distance from ladder and base of the house $ \Rightarrow b = 12 $ feet
Let AC = c be the length of the wall of the house from the base of the house till the point where the ladder touches the wall.
Since the diagram above is right angled, we can use Pythagoras theorem
That will be
 $ {a^2} = {b^2} + {c^2} $
Substituting the values we get
 $
  {20^2} = {12^2} + {c^2} \\
   \Rightarrow 400 = 144 + {c^2} \\
   \Rightarrow 400 - 144 = {c^2} \\
   \Rightarrow 256 = {c^2} \;
  $
Taking positive square root we get
 $
  c = \sqrt {256} \\
   \Rightarrow c = 16 \;
  $
Hence the value of AB i.e. the length of the wall of the house from the base of the house till the point where the ladder touches the wall is 16 feet respectively.
So, the correct answer is “16 feet”.

Note: This kind of sum can be only solved when we can construct the diagram and visualize what kind of theorem can be used. As even though a triangle is obtained, not necessarily will it always be right angled and hence we can go wrong with the answer by always applying Pythagoras theorem.