Question

The food charges in a hostel are as follows:
For the first day, the charges are Rs. 100 and for the subsequent days it is Rs. 50 per day. Taking the number of days as x and total charges as Rs. y, write a linear equation for this information and draw its graph.

Answer 1

Hint:Here first we will form a linear equation using the given information and then plot the graph of the equation using the points which satisfy the equation.
A linear equation in two variables is an equation in which the highest power of the variables is one and has two variables.

Complete step-by-step answer:
It is given that the charges for first day are Rs.100
Also, the total charges are y Rs.
Now since the total number of days are x

Therefore, the number of days on which Rs. 50 is charged are \[\left( {x - 1} \right)\]
Now, forming the linear equation we get :-

Total charges = charges on first day + charges on subsequent days
Putting the values we get:-
\[y = 100 + \left( {x - 1} \right) \times 50\]

Solving it further we get:-

\[
  y = 100 + 50x - 50 \\
  y = 50x + 50 \\
 \]

Hence the linear equation is:
\[y = 50x + 50\]

Now, plotting the graph of this equation:

Let us take three values of x and y such that they satisfy the above equation we get:

Hence plotting these points on a graph we get:-

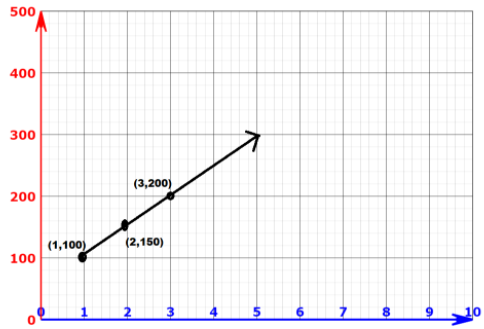
Note:Students can plot the graph using any values of x and y which satisfy the calculated linear equation.
Also, they may make mistake in forming the equation
Therefore they should use the following equation to form the equation in terms of x and y
Total charges = charges on first day + charges on subsequent days