Questions & Answers
Question
Answers
Related Questions
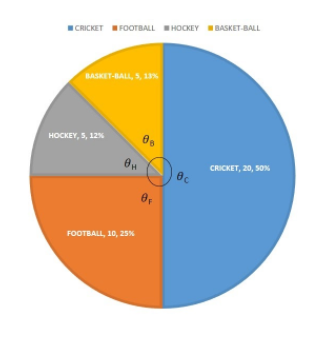
The following table shows the favourite games of 40 students in a class.
Games Cricket Football Hockey Basketball No. of Students 20 10 5 5
Represent the data using a circle graph.
| Games | Cricket | Football | Hockey | Basketball |
| No. of Students | 20 | 10 | 5 | 5 |
Answer
![Verified]()
Verified
Verified
Hint: First find the angle occupied by each game and then draw the graph.
Here, ${\theta _C},{\theta _F},{\theta _H},{\theta _B}$ are the angles occupied by Cricket, Football, Hockey and Basketball respectively.
$\theta $ is the angle, which is used to draw the graph.
Complete step-by-step answer:
To find the $\theta $ we can use this formula.
$\theta = \dfrac{{{\text{Given}}\;{\text{Quantity}}}}{{{\text{Total}}\;{\text{Quantity}}}} \times 360^\circ $
Here, the given quantity is the number of students playing each game.
Total quantity is the total no of students and $360^\circ $ is the total angle of a circle.
According to the question:
Total no of students = 40.
No. of students who play Cricket = 20.
No. of students who play Football = 10.
No. of students who play Hockey = 5
No. of students who play Basketball = 5
Now, we need to find the angle subtended by each game on the circle.
$\therefore $ angle subtended by cricket = ${\theta _c}$
${\theta _c} = \dfrac{{{2}{0}}}{{{4}{0}}} \times 360^\circ = 180$
$\therefore $ angle subtended by football = $\theta r$
${\theta _F} = \dfrac{{1{0}}}{{4{0}}} \times 360^\circ = 90^\circ $
$\therefore $ angle subtended by Hockey = \[{\theta _H}\]
\[{\theta _H} = \dfrac{5}{{{4}{0}}} \times \mathop {{3}{6}0} = 45^\circ \]
$\therefore $ angle subtended by Basketball = ${\theta _B}$
\[{\theta _B} = \dfrac{5}{{{4}{0}}} \times \mathop {{3}{6}0}= 45^\circ \]
So now, we have all the data required to draw a circle graph.
$\therefore $ the graph will be like
${\theta _C}$ = Cricket
${\theta _F}$ = Football
${\theta _H}$ = Hockey
${\theta _B}$ = Basketball
Note: In the question where the graph is required to draw.
We will 1st process the data. Also we could have made this by finding the percentage covered by each game.
Like the area covered by cricket = Ac.
Ac \[ = \dfrac{{{2}{0}}}{{4{0}}} \times \mathop {1{0}{0}} = 50\% \] area.
Similarly
AF = $\dfrac{{1{0}}}{{4{0}}} \times 100 = 25\% $ area.
AH = $\dfrac{5}{{\mathop {{4}{0}}\limits_2 }} \times \mathop {{1}{0}{0}} = \dfrac{{25}}{2} = 12.5\% $. area
AB = $\dfrac{5}{{40}} \times 100 = 12.5\% $ area
Here, ${\theta _C},{\theta _F},{\theta _H},{\theta _B}$ are the angles occupied by Cricket, Football, Hockey and Basketball respectively.
$\theta $ is the angle, which is used to draw the graph.
Complete step-by-step answer:
To find the $\theta $ we can use this formula.
$\theta = \dfrac{{{\text{Given}}\;{\text{Quantity}}}}{{{\text{Total}}\;{\text{Quantity}}}} \times 360^\circ $
Here, the given quantity is the number of students playing each game.
Total quantity is the total no of students and $360^\circ $ is the total angle of a circle.
According to the question:
Total no of students = 40.
No. of students who play Cricket = 20.
No. of students who play Football = 10.
No. of students who play Hockey = 5
No. of students who play Basketball = 5
Now, we need to find the angle subtended by each game on the circle.
$\therefore $ angle subtended by cricket = ${\theta _c}$
${\theta _c} = \dfrac{{{2}{0}}}{{{4}{0}}} \times 360^\circ = 180$
$\therefore $ angle subtended by football = $\theta r$
${\theta _F} = \dfrac{{1{0}}}{{4{0}}} \times 360^\circ = 90^\circ $
$\therefore $ angle subtended by Hockey = \[{\theta _H}\]
\[{\theta _H} = \dfrac{5}{{{4}{0}}} \times \mathop {{3}{6}0} = 45^\circ \]
$\therefore $ angle subtended by Basketball = ${\theta _B}$
\[{\theta _B} = \dfrac{5}{{{4}{0}}} \times \mathop {{3}{6}0}= 45^\circ \]
So now, we have all the data required to draw a circle graph.
$\therefore $ the graph will be like
${\theta _C}$ = Cricket
${\theta _F}$ = Football
${\theta _H}$ = Hockey
${\theta _B}$ = Basketball
Note: In the question where the graph is required to draw.
We will 1st process the data. Also we could have made this by finding the percentage covered by each game.
Like the area covered by cricket = Ac.
Ac \[ = \dfrac{{{2}{0}}}{{4{0}}} \times \mathop {1{0}{0}} = 50\% \] area.
Similarly
AF = $\dfrac{{1{0}}}{{4{0}}} \times 100 = 25\% $ area.
AH = $\dfrac{5}{{\mathop {{4}{0}}\limits_2 }} \times \mathop {{1}{0}{0}} = \dfrac{{25}}{2} = 12.5\% $. area
AB = $\dfrac{5}{{40}} \times 100 = 12.5\% $ area
Like this
Liked
-
LIVECourses
-
V PRO
-
JEE
-
JEE Main & Advanced 2020
-
JEE Main & Advanced 2021
-
JEE Main & Advanced 2022
-
-
NEET
-
NEET 2020
-
NEET 2021
-
NEET 2022
-
-
CBSE
-
Class 6
-
Class 7
-
Class 8
-
Class 9
-
Class 10
-
Class 11
-
Class 12
-
-
ICSE
-
Class 9
-
Class 10
-
-
Maharashtra Board
-
Class 9
-
Class 10
-
-
Micro Courses
-
NDA
-
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
