Question

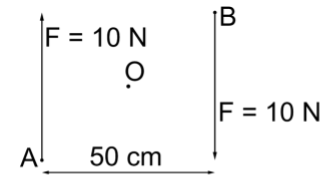
The following figure shows two forces each of magnitude $10{\text{ }}N$ acting at the points $A$ and $B$ at a separation of $50{\text{ }}cm$, in opposite directions. Calculate the resultant moment of the two forces about the point $(i){\text{ }}A$, $(ii){\text{ }}B$ and $(iii){\text{ }}O$ situation exactly at the middle of the two forces.

Answer 1

Hint: We will use the formula for torque. Then, we will put in the proper values. Finally, we will evaluate the answers for all the three questions separately and the most important part is that we will try and apply the same concept throughout for the reduction of confusions.

Formula Used:
$\vec \tau {\text{ }} = {\text{ }}\vec r{\text{ }} \times {\text{ }}\vec F{\text{ }} = {\text{ }}Fr\sin \theta $

Complete step by step answer:
In this question, the total force or precisely the total torque on any of the points can be broken down as the torque on the point due to force from $A$ added with the force from $B$. Thus, we may write this as
\[{\tau _{net}}{\text{ }} = {\text{ }}{r_1}{F_1}{\text{ }} + {\text{ }}{r_2}{F_2}{\text{ }} - - - - - - - - - - - {\text{ }}(i)\]
Where, ${r_1}$ is the perpendicular distance of the point from the line of force of $A$, ${F_1}$ is the force from $A$, ${r_2}$ is the perpendicular distance of the point from the force line of $B$ and ${F_2}$ is the force from $B$. Keeping this in mind, we proceed with the first part of the question where we are asked to find the total force or speaking precisely, the total torque on the point $A$.

Now, the torque on the point $A$ can be evaluated using the values of ${r_1}$, ${r_2}$, ${F_1}$ and ${F_2}$ as
${r_1}{\text{ }} = {\text{ }}0$
This is because the distance of point $A$ from point $A$ is quite intuitively zero.
\[{r_2}{\text{ }} = {\text{ }}50{\text{ }}cm{\text{ }} \\
\Rightarrow {r_2}{\text{ }} = {\text{ }}50{\text{ }} \times {\text{ }}{10^{ - 2}}{\text{ }}m{\text{ }} \\
\Rightarrow {r_2}{\text{ }} = {\text{ }}5{\text{ }} \times {\text{ }}{10^{ - 1}}{\text{ }}m\]
We are using the values in S.I. units as this will reduce our length of calculation and also save our time.
${F_1}{\text{ }} = {\text{ }}10{\text{ }}N$
Also,
${F_2}{\text{ }} = {\text{ }}10{\text{ }}N$
Substituting the values in equation $(i)$, we get
${\tau _A}{\text{ }} = {\text{ }}0{\text{ }} \times {\text{ }}10{\text{ }} + {\text{ }}5{\text{ }} \times {\text{ }}{10^{ - 1}}{\text{ }} \times {\text{ }}10{\text{ }} \\
\Rightarrow {\tau _A}{\text{ }}= {\text{ }}5{\text{ }}Nm$

Similarly we proceed for the second part where we are asked to find the total force or speak precisely, the total torque on the point $B$. Now, the torque on the point $B$ can be evaluated using the values of ${r_1}$, ${r_2}$, ${F_1}$ and ${F_2}$ as
${r_1}{\text{ }} = {\text{ }}5{\text{ }} \times {\text{ }}{10^{ - 1}}{\text{ }}m\\$
$\Rightarrow {r_2}{\text{ }} = {\text{ }}0 $
This is because the distance of point $B$ from point $B$ is quite intuitively zero.
${F_1}{\text{ }} = {\text{ }}10{\text{ }}N$
Also, ${F_2}{\text{ }} = {\text{ }}10{\text{ }}N$
Substituting the values in equation $(i)$, we get
${\tau _B}{\text{ }} = {\text{ }}5{\text{ }} \times {\text{ }}{10^{ - 1}}{\text{ }} \times {\text{ }}10{\text{ }} + {\text{ }}0{\text{ }} \times {\text{ }}10{\text{ }} \\
\Rightarrow {\tau _B}{\text{ }}= {\text{ }}5{\text{ }}Nm$

Also, we proceed for the second part where we are asked to find the total force or speaking precisely, the total torque on the point $O$.Now, the torque on the point $O$ can be evaluated using the values of ${r_1}$, ${r_2}$, ${F_1}$ and ${F_2}$ as the point $O$ is exactly at the middle of the two forces.Thus,
${r_1}{\text{ }} = {\text{ }}{r_2}{\text{ }} \\
\Rightarrow {r_1}{\text{ }}= {\text{ }}25{\text{ }}cm{\text{ }} \\
\Rightarrow {r_1}{\text{ }}= {\text{ }}25{\text{ }} \times {\text{ }}{10^{ - 2}}{\text{ }}m{\text{ }} \\
\Rightarrow {r_1}{\text{ }}= {\text{ }}2.5{\text{ }} \times {\text{ }}{10^{ - 1}}{\text{ }}m$
$\Rightarrow {F_1}{\text{ }} = {\text{ }}10{\text{ }}N$
Also,
${F_2}{\text{ }} = {\text{ }}10{\text{ }}N$
Substituting the values in equation $(i)$, we get
${\tau _O}{\text{ }} = {\text{ }}2.5{\text{ }} \times {\text{ }}{10^{ - 1}}{\text{ }} \times {\text{ }}10{\text{ }} + {\text{ }}2.5{\text{ }} \times {\text{ }}{10^{ - 1}}{\text{ }} \times {\text{ }}10{\text{ }} \\
\therefore {\tau _O}{\text{ }} = {\text{ }}5{\text{ }}Nm$

Hence, the answers are $(i){\text{ }}5{\text{ }}Nm$, $(ii){\text{ }}5{\text{ }}Nm$ and $(iii){\text{ }}5{\text{ }}Nm$.

Note: Students should always remember that all the values should be taken in S.I. units as this will reduce the amount of calculations to be performed as the final answer will directly come out in S.I. units. Students should be very cautious of the exponents of $10$.