Question

The following figure shows a victory stand whose dimensions are given in cm. If the bottom of the stand is open, find its volume and total surface area.
A.192000, 15000
B.162000, 15000
C.152000, 15000
D.132000, 15000

Answer 1

Hint: Here, we will first divide the stand into 13 surfaces. We will find the area of each surface and add them to find the total surface area. Then we will divide the stand into 3 cuboids and find the volume of each cuboid. We will add all the volumes to find the volume of the stand.
Formulas used:
We will use the following formulas:
1.Area of a rectangle is length times its breadth:
\[A = l \times b\]
2.Volume of a cuboid is the product of its length, breadth and height:
\[V = l \times b \times h\]

Complete step-by-step answer:
We will draw figures showing the side view of the stand:

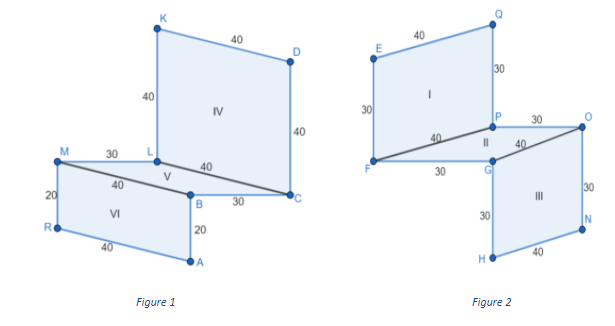
We will draw figures showing the front view and the back view of the stand:

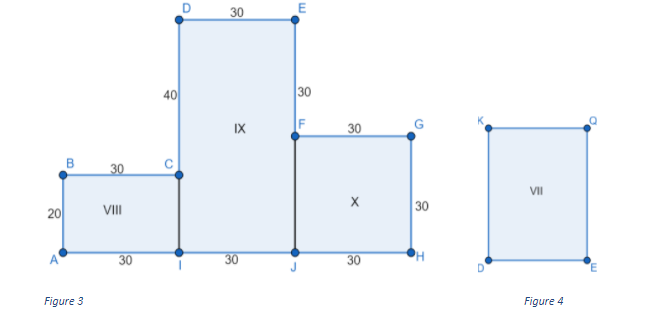
We will draw a figure showing the back view of the stand:

We will find the volume of the stand. It will be the sum of the volumes of cuboids ABCI, IDEJ and JFGH. The volume of a cuboid is the product of its length, breadth and width. We can see from figure 2 and figure 3 that the width of all 3 cuboids is 40 cm. We will find the volume of each cuboid:
\[\begin{array}{l} \Rightarrow {V_{ABCI}} = 30 \times 20 \times 40\\ \Rightarrow {V_{ABCI}} = 24000\end{array}\]
We can see from figure 1 that the length of side ID is the sum of lengths of IC and CD and the length of IJ is 30 cm:
\[ \Rightarrow {V_{IDEJ}} = 30 \times \left( {20 + 40} \right) \times 40\]
Multiplying the terms, we get
\[\begin{array}{l} \Rightarrow {V_{IDEJ}} = 30 \times 60 \times 40\\ \Rightarrow {V_{IDEJ}} = 72000\end{array}\]
Now we will find the volume of cuboid JFGH. Therefore, we get
\[\begin{array}{l} \Rightarrow {V_{JFGH}} = 30 \times 30 \times 40\\ \Rightarrow {V_{JFGH}} = 36000\end{array}\]
We will calculate the volume of the stand:
\[ \Rightarrow V = {V_{ABCI}} + {V_{IDEJ}} + {V_{JFGH}}\]
Substituting the values all the volumes of above equation, we get
\[ \Rightarrow V = 24000 + 72000 + 36000\]
Adding the terms, we get
\[ \Rightarrow V = 132000\]
$\therefore $ The volume of the stand is 132000 cubic centimetres.
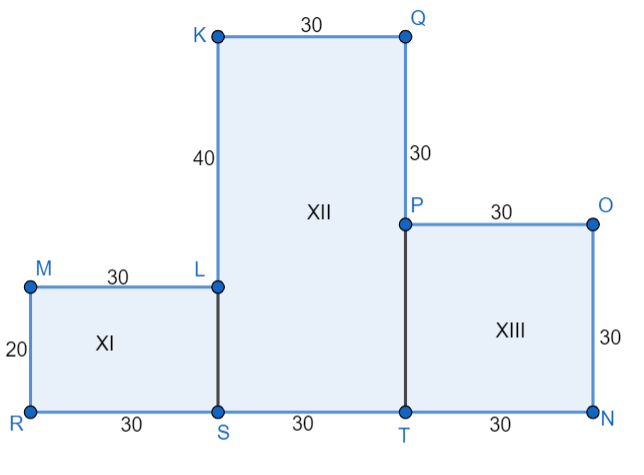
We will find the surface area of the stand. It will be the sum of the areas of figures I, II, III, IV, V, VI, VII, VIII, IX, X, XI, XII and XIII. The area of a rectangle is the product of its length and breadth. We will find the area of all the figures:
\[\begin{array}{l} \Rightarrow {A_I} = 30 \times 40\\ \Rightarrow {A_I} = 1200\\ \Rightarrow {A_{II}} = 30 \times 40\\ \Rightarrow {A_{II}} = 1200\\ \Rightarrow {A_{III}} = 30 \times 40\\ \Rightarrow {A_{III}} = 1200\\ \Rightarrow {A_{IV}} = 40 \times 40\\ \Rightarrow {A_{IV}} = 1600\\ \Rightarrow {A_V} = 30 \times 40\\ \Rightarrow {A_V} = 1200\\ \Rightarrow {A_{VI}} = 40 \times 20\\ \Rightarrow {A_{VI}} = 800\end{array}\]

\[\begin{array}{l} \Rightarrow {A_{VII}} = 30 \times 40\\ \Rightarrow {A_{VII}} = 1200\\ \Rightarrow {A_{VIII}} = 20 \times 30\\ \Rightarrow {A_{VIII}} = 600\\ \Rightarrow {A_{IX}} = 30 \times 60\\ \Rightarrow {A_{IX}} = 1800\\ \Rightarrow {A_X} = 30 \times 30\\ \Rightarrow {A_X} = 900\\ \Rightarrow {A_{XI}} = 30 \times 20\\ \Rightarrow {A_{XI}} = 600\end{array}\]

\[\begin{array}{l} \Rightarrow {A_{XII}} = 30 \times 60\\ \Rightarrow {A_{XII}} = 1800\\ \Rightarrow {A_{XIII}} = 30 \times 30\\ \Rightarrow {A_{XIII}} = 900\end{array}\]
We will calculate the total surface area
\[\begin{array}{l} \Rightarrow A = 1200 + 1200 + 1200 + 1600 + 1200 + 800 + 1200 + 600 + 1800{\rm{ + 900 + 600 + 1800 + 900}}\\ \Rightarrow A = 15000\end{array}\]
 The total surface area of the stand is 15000 square centimetres.
Option D is the correct option.

Note: We can see from symmetry that area of figure VII and XI, IX and XII and X and XIII is the same. We can calculate the area of only one figure from each pair skip calculating the area of the other figure. We must not get confused between are and volume. Area is found out for a two dimensional shape, whereas volume is found out for a three dimensional surface.