
The following are the rectangles. Find the unknown angle.
(I)
(II)


Answer
516.3k+ views
Hint: The diagonals of a rectangle are equal and bisect each other. Opposite sides of a rectangle are equal. We use the properties of angle when two straight lines intersect at a point. At least one of the angles is required to get the angles subtended by the diagonals of the rectangle.
Complete step by step solution:
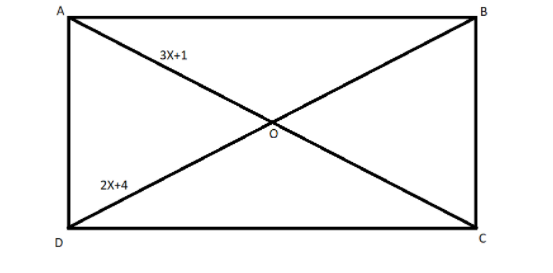
I.We are given the rectangle below.
We see that the variables are the length of the diagonals, there are no angle measure given for any of the angles and so it is impossible to get the unknown angles made by the two diagonals of the rectangle.
However the properties of the rectangle states that the angle made between the two adjacent sides of a rectangle is equal to the right angle. That is \[90^\circ \] .
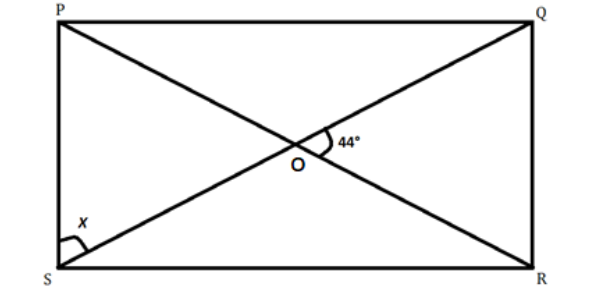
We are given the rectangle below.
II.We are given the angle made by the diagonals of the triangle.
\[ROQ = 44^\circ \]
As \[\angle ROQ\] And \[\angle POS\] are vertically opposite angle so \[\angle POS = \angle ROQ\]
So we have \[\angle POS = 44^\circ \]
Now we know that the diagonals of a rectangle bisect each other,
So in \[\Delta POS\]
\[OP = OS\] So \[\Delta POS\] is an isosceles triangle
And As the angle opposite to the equal sides of the isosceles triangle are also equal so, \[\angle OPS = \angle OSP\]
Provide that \[\angle OSP = x\]
This implies \[\angle OPS = \angle OSP = x\]
By triangle sum property we have sum of all the angles of triangle is equal to \[180^\circ \]
That is
\[\angle OPS + \angle OSP + \angle POS = 180^\circ \]
Putting the respective values
\[x + x + 44^\circ = 180^\circ \]
\[ \Rightarrow 2x + 44^\circ = 180^\circ \]
Simplifying for \[x\] keeping constant term in RHS We get,
\[ \Rightarrow 2x = 180^\circ - 44^\circ \]
On subtracting
\[ \Rightarrow 2x = 136^\circ \]
Dividing both sides by \[2\]
\[ \Rightarrow \dfrac{{2x}}{2} = \dfrac{{136^\circ }}{2}\]
\[x = 68^\circ \]
Hence the unknown angle is of \[68^\circ \].
Note: The triangles made square by its diagonal are all congruent to each other. The line intersecting two parallel lines is said to be a transverse line. The vertically opposite triangles made by the diagonal of the rectangle are congruent. It must be noted that all the angles of the rectangle are \[90^\circ \] .
Complete step by step solution:
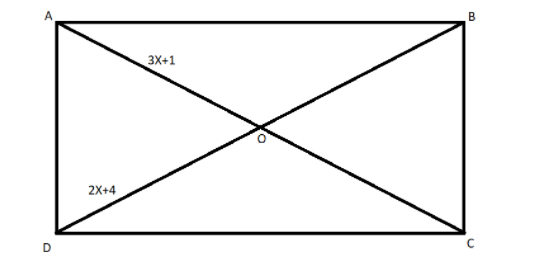
I.We are given the rectangle below.

We see that the variables are the length of the diagonals, there are no angle measure given for any of the angles and so it is impossible to get the unknown angles made by the two diagonals of the rectangle.
However the properties of the rectangle states that the angle made between the two adjacent sides of a rectangle is equal to the right angle. That is \[90^\circ \] .
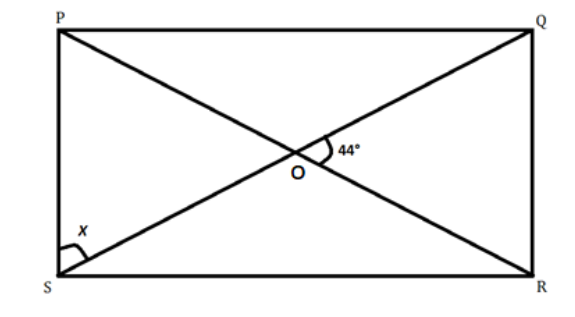
We are given the rectangle below.

II.We are given the angle made by the diagonals of the triangle.
\[ROQ = 44^\circ \]
As \[\angle ROQ\] And \[\angle POS\] are vertically opposite angle so \[\angle POS = \angle ROQ\]
So we have \[\angle POS = 44^\circ \]
Now we know that the diagonals of a rectangle bisect each other,
So in \[\Delta POS\]
\[OP = OS\] So \[\Delta POS\] is an isosceles triangle
And As the angle opposite to the equal sides of the isosceles triangle are also equal so, \[\angle OPS = \angle OSP\]
Provide that \[\angle OSP = x\]
This implies \[\angle OPS = \angle OSP = x\]
By triangle sum property we have sum of all the angles of triangle is equal to \[180^\circ \]
That is
\[\angle OPS + \angle OSP + \angle POS = 180^\circ \]
Putting the respective values
\[x + x + 44^\circ = 180^\circ \]
\[ \Rightarrow 2x + 44^\circ = 180^\circ \]
Simplifying for \[x\] keeping constant term in RHS We get,
\[ \Rightarrow 2x = 180^\circ - 44^\circ \]
On subtracting
\[ \Rightarrow 2x = 136^\circ \]
Dividing both sides by \[2\]
\[ \Rightarrow \dfrac{{2x}}{2} = \dfrac{{136^\circ }}{2}\]
\[x = 68^\circ \]
Hence the unknown angle is of \[68^\circ \].
Note: The triangles made square by its diagonal are all congruent to each other. The line intersecting two parallel lines is said to be a transverse line. The vertically opposite triangles made by the diagonal of the rectangle are congruent. It must be noted that all the angles of the rectangle are \[90^\circ \] .
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE





