Question

The focal length of a plane mirror is ______
A. Positive
B. Negative
C. Zero
D. Infinite

Answer 1

Hint: Study about both plane and spherical mirrors. Study about the reflection laws. Learn the mirror equation and try to get the focal length of the plane mirror using the equation.

Formula used:
$\dfrac{1}{f}=\dfrac{1}{u}+\dfrac{1}{v}$

Complete Step-by-Step solution:
A mirror is a reflecting surface that can reflect light. A plane mirror can be defined as a mirror with infinite radius of curvature.
Consider a spherical mirror. If we keep on increasing the radius of curvature of the spherical mirror the curvature of the mirror will decrease. If we get the infinite radius of curvature, we will get a plane mirror.
Now, the radius of curvature of a plane mirror is infinite. We can define focal length as the half of the radius of curvature. Then if the radius of curvature is infinite then the focal length will also be infinite.
We can get this by using the mirror equation for plane mirrors.

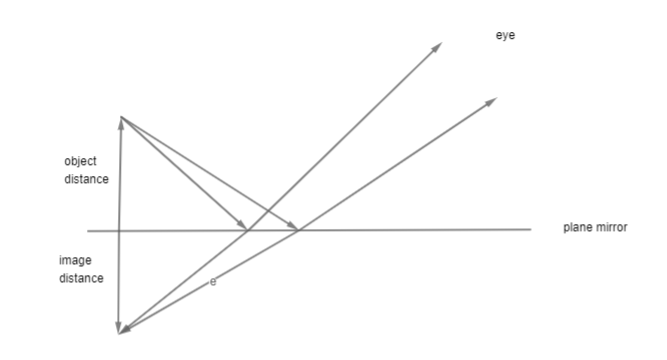
Here, light rays from the object reflected in the plane mirror and went to the observer's eye. For the observer it seems to come from behind the mirror and he sees the image formed. All of this follows the laws of reflection.
For a plane mirror,
\[\begin{align}
  & Object\text{ }distance\text{ }=\text{ - }Image\text{ }distance \\
 & u=-v \\
\end{align}\]
Using this in the mirror equation,
$\begin{align}
  & \dfrac{1}{f}=\dfrac{1}{u}+\dfrac{1}{v} \\
 & \dfrac{1}{f}=\dfrac{1}{-v}+\dfrac{1}{v} \\
 & \dfrac{1}{f}=0 \\
 & f=\dfrac{1}{0} \\
 & f=\infty \\
\end{align}$
So, the focal length of the plane mirror is infinite.

Note: The laws of reflection are the same for both plane mirrors and the spherical mirror. For spherical mirrors we get a definite radius of curvature. That’s why we never get infinite focal length in case of spherical mirrors.