Question

The focal chord to \[{y^2} = 64x\] is tangent to \[{\left( {x - 4} \right)^2} + {\left( {y - 2} \right)^2} = 4\] then the possible values of the slope of this chord is
A. \[0, - \dfrac{{12}}{{35}}\]
B. \[0,\dfrac{{12}}{{35}}\]
C. \[0,\dfrac{{35}}{{12}}\]
D. \[0, - \dfrac{{35}}{{12}}\]
E. \[0, - \dfrac{6}{{35}}\]

Answer 1

Hint: We will first consider the given focal chord \[{y^2} = 64x\] which is tangent to the circle. We will first find the focus of the parabola and then find the new equation of tangent to the given circle using the general form of equation, \[\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right) + 2\sqrt {1 + {m^2}} \] where \[m\] represents the slope and \[\left( {{x_1},{y_1}} \right)\] represents the coordinates of the given circle. Next, we will use the focus of parabola in the obtained new equation and find the slope of the chord.

Complete step by step Answer:

We will first consider the given data that is the focal chord is given by \[{y^2} = 64x\].
Also, the equation of the circle is given as \[{\left( {x - 4} \right)^2} + {\left( {y - 2} \right)^2} = 4\].
Now, we will construct the figure,

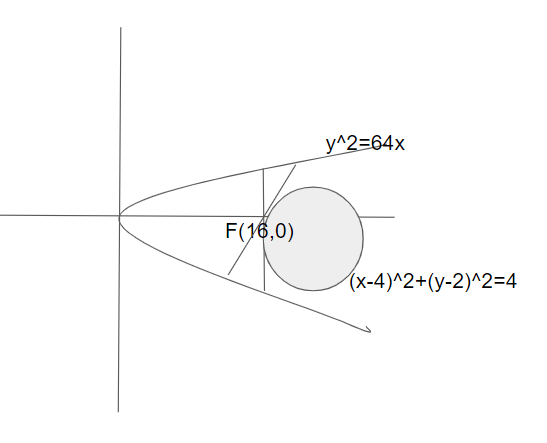
We will first find the coordinates of focus of the parabola, \[\left( {a,0} \right)\] by comparing \[{y^2} = 64x = 4\left( {16} \right)x\] with \[{y^2} = 4ax\].
Thus, we get the coordinates of the focus of parabola as;
\[ \Rightarrow S\left( {16,0} \right)\]
Now, we need to find the new equation of the tangent to the given circle using the general form of the equation that is \[\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right) + 2\sqrt {1 + {m^2}} \].
Here, we will substitute the values of the coordinates of the given circle \[\left( {{x_1},{y_1}} \right) = \left( {4,2} \right)\],
Thus, we get,
\[ \Rightarrow \left( {y - 2} \right) = m\left( {x - 4} \right) + 2\sqrt {1 + {m^2}} \]
Next, as given that the equation obtained is the focal chord of the parabola, we will substitute the point \[S\left( {16,0} \right)\] in the above equation because the focal point touches the equation of the line obtained and determine the values of the slope.
\[
   \Rightarrow \left( {0 - 2} \right) = m\left( {16 - 4} \right) + 2\sqrt {1 + {m^2}} \\
   \Rightarrow \left( { - 2} \right) = m\left( {12} \right) + 2\sqrt {1 + {m^2}} \\
 \]
Further, we will simplify the equation to determine the possible values of the slope of the chord:
Thus, we get,
\[
   \Rightarrow - 2 = 12m + 2\sqrt {1 + {m^2}} \\
   \Rightarrow - 1 = 6m + \sqrt {1 + {m^2}} \\
   \Rightarrow \left( {6m + 1} \right) = - \sqrt {1 + {m^2}} \\
 \]
Now, we will square on both sides of the equation,
\[
   \Rightarrow {\left( {6m + 1} \right)^2} = \left( {1 + {m^2}} \right) \\
   \Rightarrow 36{m^2} + 1 + 12m = 1 + {m^2} \\
   \Rightarrow 35{m^2} + 12m = 0 \\
   \Rightarrow m\left( {35m + 12} \right) = 0 \\
 \]
Here, we will apply the zero-factor property to determine the possible values of the slope.
Thus, we get,
\[ \Rightarrow m = 0\] and \[35m + 12 = 0\]
\[ \Rightarrow m = 0\] and \[m = - \dfrac{{12}}{{35}}\]
Hence, we get the possible values of the slope of the chord as \[m = 0, - \dfrac{{12}}{{35}}\].
Thus, option A is correct.

Note: Remember to find out the focus of the parabola using the given equation of parabola \[{y^2} = 64x\]. The general form of the equation of tangent to the circle is \[\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right) + 2\sqrt {1 + {m^2}} \]. We have substituted the values of \[\left( {{x_1},{y_1}} \right) = \left( {2,4} \right)\] obtained from the equation of the given circle. Squaring on both sides makes the calculation easier.