Question

The floor of a building is made up of 2550 tiles which are in the shape of a rhombus. If the diagonals of each tiles are of length 20 cm and 28 cm, find the cost of polishing the floor at the rate of Rs. 25 per $ {m^2} $

Answer 1

Hint: We can find the area of one tile according to the given data as it is rhombus in shape, the multiplication of this area with the number of tiles will give the total area to be polished. The cost of polishing $ 1{m^2} $ is given to be Rs. 25, so we need to find the total area in $ {m^2} $ , then by using the unitary method, we can find the cost of polishing the floor.
Area of rhombus = \[\dfrac{1}{2} \times {d_1} \times {d_2}\]
For conversion remember: $ 100cm = 1m $

Complete step by step solution:

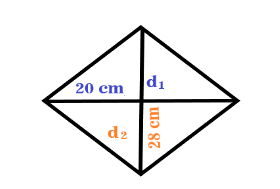
It is given that the floor is made up of 2550 tiles which are in the shape of a rhombus. The diagonals of each tiles are of length 20 cm and 28 cm
 Number of tiles (n) = 2550
 Length of the first diagonal $ \left( {{d_1}} \right) $ = 20 cm
 Length of the second diagonal $ \left( {{d_2}} \right) $ = 28 cm
The area of one tile will be equal to that of the rhombus which is given as:
Area of rhombus (A) = \[\dfrac{1}{2} \times {d_1} \times {d_2}\]
Substituting the values, we get:
\[
\Rightarrow A = \dfrac{1}{2} \times 20\;cm \times 28\;cm \\
 \Rightarrow A = 280\;c{m^2} \;
 \]
Thus, the area of one tile is equal to $ 280\;c{m^2} $ . The total area (TA) covered by these tiles on the floor can be given by the product of this area (A) with total number of tiles (n).
 $ TA = A \times n $
Substituting the values, we get:
 $
\Rightarrow TA = 280 \times 2550 \\
\Rightarrow TA = 714000 \;
  $
But, the cost of polishing is given in $ {m^2} $ , so:
 $
  714000\;c{m^2} = 71.4\;{m^2} \\
  \left( {\because 1\;m = 100\;cm} \right) \;
  $
The cost of polishing $ 1{m^2} $ is given to be Rs. 25, for $ 71.4\;{m^2} $ , it can be calculated using unitary method:
\[
  1{m^2} = Rs.25 \\
  71.4\;{m^2} = Rs.\left( {\dfrac{{25}}{1} \times 71.4} \right) \\
   \Rightarrow 71.4\;{m^2} = Rs.1785 \;
 \]
Therefore, the cost of polishing the floor at the rate of Rs. 25 per $ {m^2} $ will be Rs. 1785
So, the correct answer is “Rs. 1785”.

Note: We can also have converted the lengths of the diameter from cm to m in the beginning but as 2550 was a multiple of 5, we had an idea that the number obtained after the product might have the zeroes which will get cancelled and make the calculation easier and thus we made the conversion after finding the area.
We can do the conversion to avoid mistake as:
 $
  100cm = 1m \\
   \Rightarrow 1\;cm = \dfrac{1}{{100}}\;m \;
  $
So when we have to convert $ 714000c{m^2} $ to $ {m^2} $ , we can do it as:
 $
  714000\;c{m^2} \times \dfrac{{1{m^2}}}{{100c{m^2}}} \times \dfrac{{1{m^2}}}{{100c{m^2}}} \\
   \Rightarrow 71.4\;{m^2} \;
  $