Question

The figures shoves two concentric circles and AD is a chord of larger circle then ${\text{AB}}\;{\text{ = }}\;{\text{2CD}}$ is
1)True 2) False

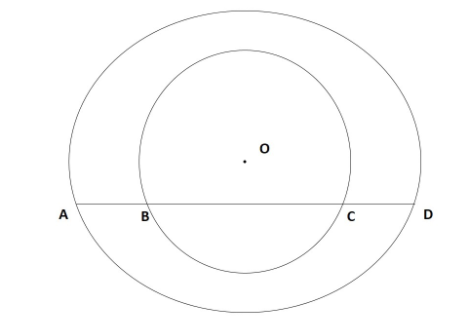
Answer 1

Hint : Chord is a segment of a circle that connects two points of a circle. One chord of a bigger circle is not necessarily the chord of a smaller circle for two concentric circles. Perpendicular from the centre of the circle will bisects the chord of that circle. Bisects means division in two equal parts. So in this type of questions use the theorem of congruent triangle for proving any kind of theorem.

Complete step-by-step answer:
We will use the following formula.
(i)Perpendicular from the center of the circle bisects the chord.
(ii)If hypotenuse and one side of two triangles are equal then both will congruent.
Now,

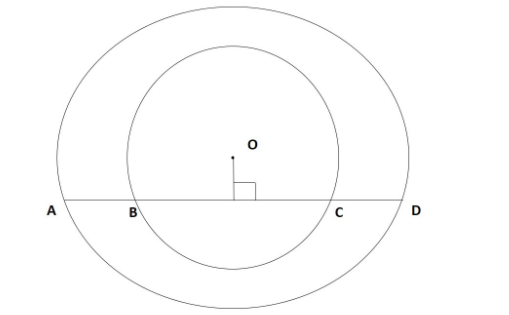
Perpendicular OE will be the radius of inner circle
So, According to theorem + from center on chord bisects the chord BC.
Now, again:
     

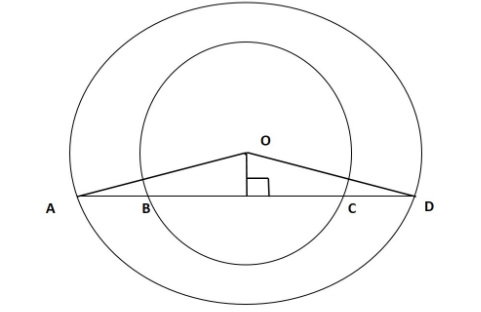
For a bigger circle AO and OD are the radius.
Both $\Delta {\text{OAE}}\;{\text{ = }}\;{{\Delta OED}}\;\left( {\text{as}}\;\,{\text{OA = OD}} \\
  \;\;\;\;{\text{OE = OE}} \\
\right)$
So, $AE\; = \;ED\;$ $\; < OEA = \; < OED = {90^ \circ }$
AE can be written as ${\text{AB}}\;{\text{ + }}\;{\text{BE}}\;\;\;{\text{and}}\;{\text{ED}}\;{\text{ = }}\;{\text{EC}}\;{\text{ + CD}}\;{\text{as}}\;{\text{BE}}\;{\text{ = }}\;{\text{EC}}$
So, \[{\text{AB = }}\;{\text{CD}}\]
Hence, \[{\text{AB}}\;{\text{ = }}\;{\text{2CD}}\] (False).

Note : Concentric circles have a common centre so perpendicular from that centre will be the radius of the circle and the radius of the bigger circle will be the hypotenuse of those right angle triangles as shown in figure. Two concentric circles have a chord running through the outer one. The chord is the tangent of the inner circle, but this condition is not always necessary but it can be used in some other problems.