Question

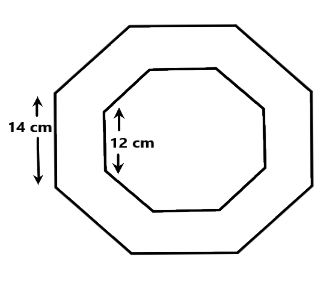
The figure shows the diagram of a regular octagon-shaped frame. The length of the side of the inner octagon is $12\,cm$ and the outer octagon is $14\,cm$. Find the area of the frame if the width of the frame is the same at all sides?

Answer 1

Hint:Here in this question, we have to find the area of the given regular octagon-shaped frame. The frame having a inner and outer octagon shape then find its area by using a formula \[A = 2\left( {1 + \sqrt 2 } \right){a^2}\], where ‘\[a\]’ is the length of any one side of the octagon and further by taking a difference of area of inner and outer octagon to get the required solution.

Complete step by step answer:
In geometry, Area can be defined as the region or space occupied by a geometric figure or shape. A regular octagon is a type of polynomial whose eight sides are equal in length, and eight angles are of equal measures. The formula of area of the regular octagon is: \[A = 2\left( {1 + \sqrt 2 } \right){a^2}\]------(1)
Where ‘\[a\]’ is the length of any one side of the octagon.

Now, consider the question:
Given a diagram of a regular octagon-shaped frame, we have to find the area of the frame if the width of the frame is the same at all sides. The diagram of the frame had an inner octagon of 12 cm length and outer octagon of 14 cm length both are regular. Now find the area of outer octagon of length \[a = 14\], then by the formula, we have
\[{A_1} = 2\left( {1 + \sqrt 2 } \right){\left( {14} \right)^2}\]
\[ \Rightarrow \,\,\,{A_1} = 2\left( {1 + \sqrt 2 } \right)\left( {196} \right)\]
\[\therefore \,\,\,{A_1} = 392\left( {1 + \sqrt 2 } \right)\,\,\,c{m^2}\] --------(2)

Now find the area of inner octagon of length \[a = 12\], then
By the formula, we have
\[{A_2} = 2\left( {1 + \sqrt 2 } \right){\left( {12} \right)^2}\]
\[ \Rightarrow \,\,\,{A_2} = 2\left( {1 + \sqrt 2 } \right)\left( {144} \right)\]
\[\therefore \,\,\,{A_2} = 288\left( {1 + \sqrt 2 } \right)\,\,\,c{m^2}\] --------(2)
The area of the given regular octagonal-shaped frame is:
\[ \Rightarrow \,\,\,\]Area of outer octagon \[ - \] Area of inner octagon
\[ \Rightarrow \,\,\,A = 392\left( {1 + \sqrt 2 } \right) - 288\left( {1 + \sqrt 2 } \right)\]
Take out common term \[\left( {1 + \sqrt 2 } \right)\], then
\[ \left( {1 + \sqrt 2 } \right)\left( {392 - 288} \right)\]
\[ \Rightarrow \,\,\,\left( {1 + \sqrt 2 } \right)\left( {104} \right)\]
Apply a distributive property
\[104 + 104\sqrt 2 \]
\[ \Rightarrow \,\,\,104 + 147.078\]
\[\therefore \,\,\,251.078\,\,\,\,c{m^2}\]

Hence, the approximate area of the given regular octagonal-shaped frame is \[251\,\,\,c{m^2}\].

Note: Remember, In the regular shaped polygon the length of all sides and angles between any two sides are always equal and in measurement based questions, you should not forget to write the unit with the final answer. Whereas the unit for the area will be the square of the unit of the length of the side of a polygon.