Question

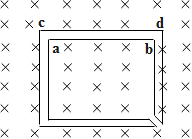
The figure shows certain wire segments joined together to form a coplanar loop. The loop is placed in a perpendicular magnetic field in the direction going into the plane of the figure. The magnitude of the field increases with time. ${{\text{I}}_{\text{1}}}\text{ and }{{\text{I}}_{\text{2}}}$ are the currents in segment ab and cd. Then:

A) I₁ > I₂
B) I₁ < I₂
C) ${{\text{I}}_{\text{1}}}$ is in the direction ba and$\text{ }{{\text{I}}_{\text{2}}}$ is in the direction cd.
D) ${{\text{I}}_{\text{1}}}$ is in the direction ab and$\text{ }{{\text{I}}_{\text{2}}}$ is in the direction dc.

Answer 1

Hint: In the above diagram we can see that the loop is placed in a varying magnetic field pointing towards the inner side. Since the magnetic field keeps on changing with time, the flux through the loop will keep on changing resulting in an induced emf in the loop. When there is a changing magnetic field across a given cross section, from Lenz law we can say that the loop will generate a magnetic field opposite to the applied field in order to nullify the changing magnetic field. Hence we will detriment the magnetic field by the right hand rule for closed loops.

Complete answer:
In the above figure, the loop is basically a closed one. Hence whatever current flows through it will be flowing through the entire loop.

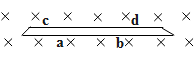
The above figure is an equivalent to that given to us in the question. We have basically made the loop straight. Now since the loop is kept in changing magnetic field, by Lenz law the loop will generate its own magnetic field in the opposite direction to the applied in order to oppose the changing magnetic field.
Let us say we curl the fingers of our right hand such that all the four fingers point to the direction of current in the loop. Then the thumb pointing outwards perpendicular to the plane of the fingers indicates the direction of the magnetic field. The magnetic field as per Lenz law, has to be outwards as the changing field directs inwards. If we place the thumb such that it points outwards, the fingers will be directed from d to c and then from a to b.
In the question it is given to us that ${{\text{I}}_{\text{1}}}\text{ and }{{\text{I}}_{\text{2}}}$ are the currents in segment ab and cd.
Hence ${{\text{I}}_{\text{1}}}$will flow in direction of ab and ${{\text{I}}_{\text{2}}}$will flow in the direction of dc.

So, the correct answer is “Option D”.

Note:
The emf is induced in the circuit when there is change in flux ($\phi $ )across the cross section A. Flux is defined as $\phi =BA$ where B is the magnetic field perpendicular to A. The change in flux with time gives us the induced emf. Hence differentiating the equation of flux with respect to time we get,
$\dfrac{d\phi }{dx}=B\dfrac{dA}{dx}+A\dfrac{dB}{dx}$
From the above equation we can conclude that if either the area of the cross section or the magnetic field across the cross section changes then there will be an induced emf.