Question

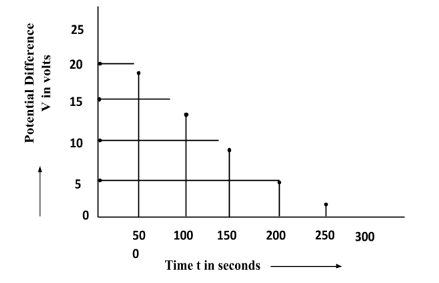
The figure shows an experimental plot for discharging of a capacitor in an RC circuit. The time constant $\tau$ of this circuit lies between:

A. 150 sec and 200 sec
B. 0 and 50 sec
C. 50 sec and 100 sec
D. 100 sec and 150 sec

Answer 1

Hint: To solve this problem, use the formula for discharging of a capacitor. Assume that, the voltage across the capacitor is half of the maximum voltage that the capacitor can attain. Substitute this assumed value in the equation for discharging of a capacitor. This will give the value of time constant in terms of time t. From, the graph given, chose the time at which the voltage across the capacitor is half of the maximum voltage. Substitute that value of time in the expression for time constant which you calculated. This will give the range in which time constant of the circuit lies.

Complete answer:
Discharging of a capacitor in a RC circuit is given by,
$V = {V}_{0} (1- {e}^{(- \dfrac {t}{\tau})})$ …{1}
Where, V be the voltage across the capacitor
             ${V}_{0}$ is the maximum voltage
             $\tau$ is the time constant
Let $V= \dfrac {{V}_{0}}{2}$
Substituting this value in the equation. (1) we get,
$ \dfrac {{V}_{0}}{2}= {V}_{0} (1- {e}^{(- \dfrac {t}{\tau})})$
$\rightarrow \dfrac {1}{2}= 1- {e}^{(- \dfrac {t}{\tau})}$
$\rightarrow \dfrac {1}{2}= {e}^{(- \dfrac {t}{\tau})}$
Taking the natural log on both the sides we get,
$ln\dfrac{1}{2}= - \dfrac {t}{\tau}$
$\Rightarrow \tau = \dfrac {t}{ln2}$ …(2)
From the graph, we can infer that at t=100, V= 12.5V, which is the half of the maximum voltage i.e. $V= \dfrac{{V}_{0}}{2}$
Thus, substituting t= 100 in the equation. (2) we get,
$ \tau = \dfrac {100}{ln2}$
$\Rightarrow \tau = \dfrac {100}{0.69}$
$\Rightarrow \tau = 144.93$
Hence, the time constant of this circuit lies between 100 sec and 150 sec.

So, the correct answer is “Option D”.

Note:
During charging of the capacitor, when time t equals one time constant ($\tau$), the charge on the capacitor becomes 37% of the initial charge. While discharging the capacitor, when the time t equals one time constant ($\tau$), the charge on the capacitor becomes 63% of the maximum charge. It takes four time constants i.e. $4\tau$, for the capacitor to get completely charged. Even though the capacitor gets fully charged at four time constant, the time constant can have further values as well such as $5\tau$, $6\tau$ and so on.