Question

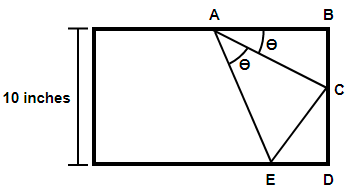
The figure shows a long rectangular strip of paper one corner of which has been folded over along the AC to meet the opposite edge, thereby creating angle $\theta \left( \angle CAB \right)$. Given that the width of the strip is 10 inches, find the length of the crease AC in terms of $\theta $.

Answer 1

Hint: Draw a perpendicular from A to the opposite side of the rectangle and name it as AP. In the right triangle APE find the value of angle AEP and take sine of that angle to form a relation between the sides AE and AP. Now, in the right triangle ABC find the value of cosine of the angle $\theta $ and form a relation between AB and AC. Consider AE = AB and replace the value of AE in the first relation to get the answer. The value of AP is equal to the width of the rectangle, i.e. 10 inches.

Complete step by step answer:
Here we have been provided with the figure in which a strip of rectangular paper has been folded from one corner to meet the opposite edge. We are asked to find the value of the crease AC if the width of the rectangle is 10 inches.

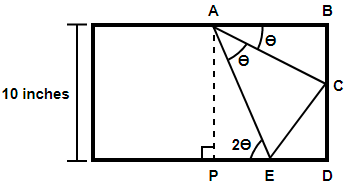
Now, in the above figure we have drawn a perpendicular AP. The length of AP will be equal to the width of the rectangular paper because ABDP can be considered as a small triangle and we know that the opposite sides of a rectangle are equal. Since the provided width of the rectangle is 10 inches, so we have AP = 10 inches.
We have been given $\angle CAB=\theta $ so $\angle CAE=\theta $ because triangle CAB and CAE are same triangles. Therefore in right triangle APE we get $\angle PAE=\left( {{90}^{\circ }}-2\theta \right)$ which results in $\angle AEP=2\theta $. So in right triangle APE for angle $2\theta $ we have AP and AE as the perpendicular and hypotenuse respectively, therefore we get,
$\Rightarrow \sin 2\theta =\dfrac{AP}{AE}$
Clearly we can see that AE = AB because the length AB after getting folded will become AE, so we get,
$\begin{align}
  & \Rightarrow \sin 2\theta =\dfrac{10}{AB} \\
 & \Rightarrow AB=\dfrac{10}{\sin 2\theta }.......\left( i \right) \\
\end{align}$
Now, in the right triangle ABC for angle $\theta $ we have the sides AB and AC as the base and hypotenuse respectively, therefore we have,
$\begin{align}
  & \Rightarrow \cos \theta =\dfrac{AB}{AC} \\
 & \Rightarrow AC=\dfrac{AB}{\cos \theta }........\left( ii \right) \\
\end{align}$
Substituting the value of AB from equation (i) in equation (ii) we get,
$\therefore AC=\dfrac{10}{\sin 2\theta \cos \theta }$
Hence, the length of the crease AC is $\dfrac{10}{\sin 2\theta \cos \theta }$.

Note: From the obtained relation of the crease AC you can find its length for any angle suitable angle $\theta $. The folded angle will not be more than ${{45}^{\circ }}$otherwise point E will not touch the opposite side. You can determine the minimum length of the crease by differentiating the obtained relation with respect to the angle $\theta $ then substituting it equal to 0. The obtained value of $\theta $ will be put in the relation of AC to get the minimum length.