Question

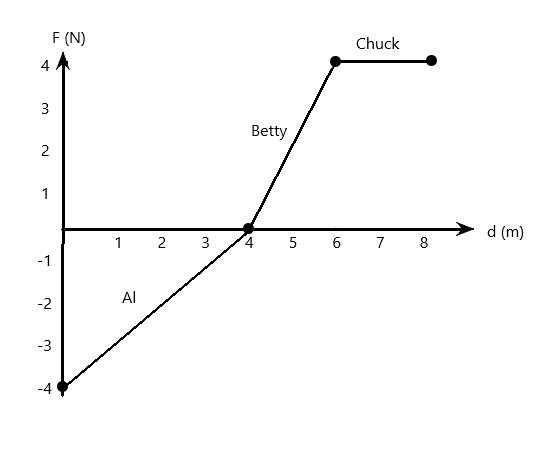
The figure below is a force vs displacement graph showing the amount of force applied to an object by three different people. Al applies force to the object for the first 4m of its displacement, Betty applies force from the 4m point to the 6m point, chuck applies force from the 6m point to the 8m point which of the three does the most work on the object?

A. Al
B. Betty
C. Chuck
D. Ai and Chuck do the same amount of work.

Answer 1

Hint: The area under the curve of a force-displacement graph gives the work done. Observe that the area for Al and Betty is a triangle, and for the chuck is a rectangle.

Formula used: In this solution we will be using the following formulae;
\[{A_t} = \dfrac{1}{2}bh\] where \[{A_t}\] is the area of a triangle, \[b\] is the base of the triangle and \[h\] is the height.
\[{A_r} = lb\] where \[{A_r}\] is the area of a rectangle, \[l\] is the length of the rectangle and \[b\] is the breadth of the rectangle.

Complete step by step answer:
The graph as mentioned shows us a force displacement graph of three different people. We are to calculate which of them did more work.
In such a graph, the area under or over the curve for the section of it considered is the work done in that section of the graph.
Hence, for Al, we see a triangle. The area of a triangle can be given as
\[{A_r} = lb\] where \[{A_r}\] is the area of a rectangle, \[l\] is the length of the rectangle and \[b\] is the breadth of the rectangle.
Hence, we have
\[{W_{Al}} = \dfrac{1}{2} \times 4 \times - 4 = - 8J\]
For betty, we see another triangle, hence,
\[{W_B} = \dfrac{1}{2} \times \left( {6 - 4} \right) \times 4 = 4J\] and hence
Chuck, we see a rectangle. The area of a rectangle is given as
\[{A_r} = lb\] where \[{A_r}\] is the area of a rectangle, \[l\] is the length of the rectangle and \[b\] is the breadth of the rectangle. Thus, we have
\[{W_C} = \left( {8 - 6} \right) \times 4 = 8J\]
Hence, Al and Chuck do the same amount of work.
Hence, the correct option is D.

Note: For clarity, note that we say they do the same amount of work even though Al’s work is written as negative. This is because work done is a scalar, and the sign of the work only tells that the direction of the force and displacement are in the opposite direction. The quantity of work actually being done is the same.