Question

The extremities of a diagonal of a rectangle are (-4,4) and (6, -1). A circle circumscribes the rectangle and cuts an intercept AB on the y-axis. The area of the triangle formed by the chord AB and the tangents drawn to the circle at A and B is
[a] $1331$
[b] $\dfrac{1331}{2}$
[c] $\dfrac{1331}{4}$
[d] $\dfrac{1331}{8}$

Answer 1

Hint:Use the fact that the angle in a semicircle is right angle. Hence if a circle circumscribes a right-angled triangle, then the hypotenuse of the triangle is the diameter of the circle. Use the fact that the equation of the circle with diametric points as $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is ${{x}^{2}}+{{y}^{2}}-\left( {{x}_{1}}+{{x}_{2}} \right)x-\left( {{y}_{1}}+{{y}_{2}} \right)y+{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}=0$
Hence find the equation of the circle circumscribing the rectangle. Use the fact that the intercept of the circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ on the y-axis is $2\sqrt{{{f}^{2}}-c}$. Hence find the length AB. Use the fact that OB = r(radius of the circle) and $BF=\dfrac{1}{2}AB$. Hence find the value of $\sin \alpha $ in triangle OFB. Now in triangle OBE prove that $\cos \alpha =\dfrac{OB}{OE}$. Use the fact that ${{\sin }^{2}}x+{{\cos }^{2}}x=1$ and hence find the value of OE. Using Pythagora’s theorem in triangle OEB, find the value of EB. Using Pythagora’s theorem in triangle EFB, find the value of EF. Use the fact that the area of the triangle of base b and height h is given by $A=\dfrac{1}{2}bh$. Hence fin the area of the triangle ABE.

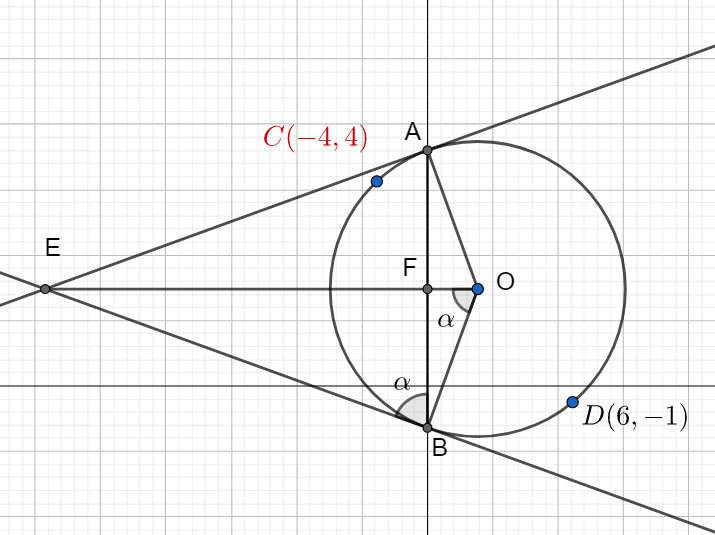
Complete step by step answer:
We know that if a right-angled triangle is circumscribed by a circle, then the hypotenuse of the triangle is the diameter of the circle. Since the diagonal of a rectangle is the hypotenuse of one of the right-angled triangles, which the circle circumscribing the rectangle also circumscribes, we have the end-points of the diagonal of a rectangle are the diametric endpoints of its circumscribing circle.
Hence, we have $C\left( -4,4 \right)$ and $D\left( 6,-1 \right)$ are the diametric endpoints of the circle circumscribing the rectangle.
We know that the equation of the circle with diametric points as $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is ${{x}^{2}}+{{y}^{2}}-\left( {{x}_{1}}+{{x}_{2}} \right)x-\left( {{y}_{1}}+{{y}_{2}} \right)y+{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}=0$
Hence, we have
Equation of the circle is
$\begin{align}
  & {{x}^{2}}+{{y}^{2}}-\left( -4+6 \right)x-\left( 4-1 \right)y-24-4=0 \\
 & \Rightarrow {{x}^{2}}+{{y}^{2}}-2x-3y-28=0 \\
\end{align}$
We know that the y-intercept of the circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ is given by $2\sqrt{{{f}^{2}}-c}$. Here $f=\dfrac{-3}{2}$ and $c=-28$
Hence, we have
$AB=2\sqrt{{{\left( \dfrac{3}{2} \right)}^{2}}+28}=\sqrt{9+112}=11$
Since the line joining the point of intersection of tangents at the endpoints of a chord of the circle and the centre of the circle is perpendicular bisector of the chord, we have
$BF=\dfrac{1}{2}AB$
Also, we know that the radius of the circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ is given by $r=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$
Hence, we have
$OB=\sqrt{{{1}^{2}}+\dfrac{9}{4}+28}=\dfrac{5\sqrt{5}}{2}$
In triangle OFB, we have
$\sin \alpha =\dfrac{BF}{OB}=\dfrac{\dfrac{11}{2}}{\dfrac{5\sqrt{5}}{2}}=\dfrac{11}{5\sqrt{5}}$
In triangle OEB, we have
$\cos \alpha =\dfrac{OB}{OE}=\dfrac{5\sqrt{5}}{2OE}$
We know that ${{\sin }^{2}}x+{{\cos }^{2}}x=1$
Hence, we have
$\begin{align}
  & {{\left( \dfrac{11}{5\sqrt{5}} \right)}^{2}}+{{\left( \dfrac{5\sqrt{5}}{2OE} \right)}^{2}}=1 \\
 & \Rightarrow \dfrac{121}{125}+\dfrac{125}{4O{{E}^{2}}}=1 \\
\end{align}$
Subtracting $\dfrac{121}{125}$ on both sides, we get
$\dfrac{125}{4O{{E}^{2}}}=\dfrac{4}{125}$
Multiplying both sides by $\dfrac{125}{4}O{{E}^{2}}$, we get
$O{{E}^{2}}={{\left( \dfrac{125}{4} \right)}^{2}}\Rightarrow OE=\dfrac{125}{4}$
In triangle OBE, by Pythagora’s theorem, we have
$\begin{align}
  & O{{B}^{2}}+B{{E}^{2}}=O{{E}^{2}} \\
 & \Rightarrow \dfrac{125}{4}+B{{E}^{2}}=\dfrac{{{125}^{2}}}{{{4}^{2}}} \\
 & \Rightarrow BE=\dfrac{55\sqrt{5}}{4} \\
\end{align}$
In triangle EFB by Pythagoras theorem, we have
$\begin{align}
  & E{{F}^{2}}+F{{B}^{2}}=E{{B}^{2}} \\
 & \Rightarrow E{{F}^{2}}+{{\left( \dfrac{11}{2} \right)}^{2}}={{\left( \dfrac{55\sqrt{5}}{4} \right)}^{2}} \\
 & \Rightarrow EF=\dfrac{121}{4} \\
\end{align}$
In triangle ABE, we have $AB=\dfrac{11}{2}$ and $EF=\dfrac{121}{4}$. We know that in a triangle if height is h and base is b, then the area of the triangle is given by $\Delta =\dfrac{1}{2}bh$
Hence, we have
$ar\left( \Delta ABE \right)=\dfrac{1}{2}EF\times AB=\dfrac{1}{2}\times 11\times \dfrac{121}{4}=\dfrac{1331}{8}$
Hence option [d] is correct.

Note:
[1] Alternatively, we can find the coordinates of point A and point B by substituting x = 0 in the equation of the circle and solving the corresponding quadratic equation. Then we can find the equations of the tangents at points A and B and hence find the coordinates of the point E. Finally we can use the property that the area of the triangle formed by points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right),C\left( {{x}_{3}},{{y}_{3}} \right)$ is given by$\Delta =\dfrac{1}{2}\left| \begin{matrix}
   {{x}_{2}}-{{x}_{1}} & {{y}_{2}}-{{y}_{1}} \\
   {{x}_{3}}-{{x}_{1}} & {{y}_{3}}-{{y}_{1}} \\
\end{matrix} \right|$ and hence find the area of the triangle ABE. This method is avoided as this method is prone to calculation mistakes.