Question

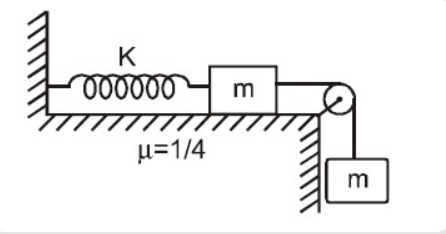
The extension in the spring when the masses come to momentary rest for the first time is

$ \left( A \right)1.5m \\
  \left( B \right)6m \\
  \left( C \right)3m \\
  \left( D \right)none of these \\ $

Answer 1

Hint :In order to solve this question, we are going to use the work energy theorem .We know that the masses stop when the total work done on them is zero. This can be found by taking the potential energy due to the height of suspended mass, the kinetic energy and the spring energy, their sum is equated to zero.
The potential energy of a box of mass $ m $ sliding on surface with coefficient of friction $ \mu $ with displacement $ x $ is $ \mu mgx $
Potential energy for mass suspended at height $ h $
 $ E = mgh $
Energy for the spring with extension $ x $ and spring constant $ k $ is
 $ E = \dfrac{1}{2}k{x^2} $

Complete Step By Step Answer:
According to the Work energy theorem, the total work done on a system is equal to the difference of its initial and final energies
Applying the theorem in this situation, we get
 $ W = mgx - \dfrac{1}{2}k{x^2} - \mu mgx = 0 $
Here, the extension $ x $ in the spring is the displacement on the surface and the height of the suspended mass also
Solving the equation, we get
$ \Rightarrow \dfrac{1}{2}k{x^2} = mgx\left( {1 - \mu } \right) \\
   \Rightarrow x = \dfrac{{2mg}}{k}\left( {1 - \mu } \right) \\ $

Now, the values of all these constants are known, so putting those in the above equation, we get
$\Rightarrow x = \dfrac{{2mg}}{k}\left( {1 - \dfrac{1}{4}} \right) \\
   \Rightarrow x = \dfrac{{2mg}}{k} \times \dfrac{3}{4} = \dfrac{{3mg}}{{2k}} \\ $
Putting the rest values in it
 $ \Rightarrow x = \dfrac{{3 \times 2 \times 10}}{{2 \times 20}} = 1.5 $
Therefore, the extension in the spring when the masses come to momentary rest for the first time is
$ 1.5m $ , option $ \left( A \right) $ .

Note :
The extension to which the spring is stretched displaces the mass on the surfaces to exactly that value only and the mass that is suspended in the air leading to a change in the potential energy to be $ mgx $ . When the work done will be zero or the initial and the final energies are equal, the masses come to rest.