Question

The equivalent resistance between points A and B is:

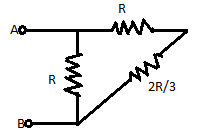
A. $R$
B. $\dfrac{R}{2}$
C. $\dfrac{{5R}}{8}$
D. $\dfrac{{2R}}{3}$

Answer 1

Hint: Here we have applied the concepts of resistance in series and parallel.
The resistance is the opposition to a current flow in a circuit. It is also defined as the ratio of voltage to current.The two resistors have a similar potential difference across them. The total current in the circuit is the whole of the flows through each branch.

Complete step by step answer:
The cumulative resistance of the series circuit is equal to the number of the individual resistances.
The voltage applied to the series circuit is proportional to the sum of the voltage drops. The voltage drop over the resistor in a series circuit is directly proportional to the size of the resistor.
In a series circuit, the output current of the first resistor flows through the input of the second resistor, thus the current in each resistor is the same.
In a parallel circuit, the entirety of the resistor leads on one side of the resistors are associated together and all the leads on the opposite side are associated together.
In a parallel circuit, the net resistance diminishes as more segments are included, on the grounds that there are more ways for the current to go through. The two resistors have a similar potential difference across them. The total current in the circuit is the whole of the flows through each branch.
The equivalent resistance of a network is the one resistor that could replace the whole network in such
a manner that we get the same current with a given applied voltage as we did for a network.

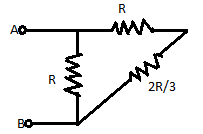
If we observe the circuit from the right hand side we can see that the resistances $R$ and $\dfrac{{2R}}{3}$ are connected in series, so the total resistance between these resistors will be
$
   = R + \dfrac{{2R}}
{3} \\
   = \dfrac{{5R}}
{3} \\
$

Now, the resistance $\dfrac{{5R}}{3}$ is connected in parallel with the resistance $R$ , so the equivalent resistance will be:
$
  \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{R} + \dfrac{3}{{5R}} \\
\implies \dfrac{1}{{{R_{eq}}}} = \dfrac{8}{{5R}} \\ {R_{eq}} = \dfrac{{5R}}{8} \\
$

So, the correct answer is “Option C”.

Note:
Here we have to carefully observe the circuit which of the resistance is connected in series and which is connected in parallel. Only then we can find the correct answer.
The net resistance diminishes as more segments are included, on the grounds that there are more ways for the current to go through.