Question

The equivalent resistance between point A and B is:

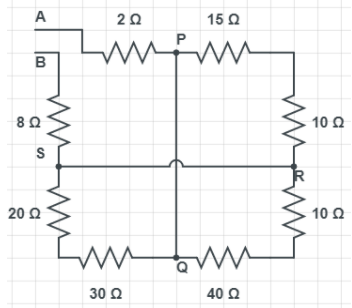
$\begin{align}
  & A.\text{ }32.5\Omega \\
 & B.\text{ }22.5\Omega . \\
 & C.\text{ }2.5\Omega \\
 & D.\text{ }42.5\Omega \\
\end{align}$

Answer 1

Hint: We have been provided with a circuit in question. Three pairs of resistance in parallel to each other and two resistances from each of the pair are in series. So apply a formula of resistance in parallel for those three pairs of resistance and then use resistance in series at point AB.

Complete answer:
The above circuit can be drawn as follows to make it easy to solve.

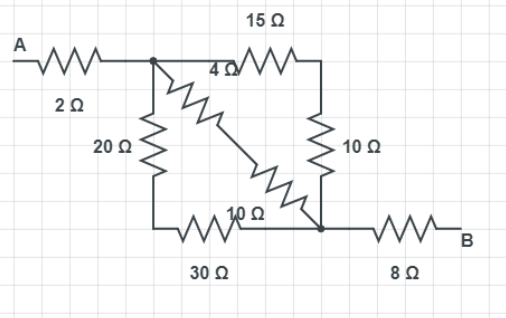
As you can see in given equivalent circuit diagram it shows the series combination of the resistance in the circuit which is $15\Omega ,\text{ 10}\Omega \text{, 40}\Omega \text{, 10}\Omega \text{, 20}\Omega \text{, 30}\Omega \text{.}$. Let ${{R}_{1}}$ be the equivalent resistance of the series combination of resistance $15\Omega ,\text{ 10}\Omega \text{.}$ Similarly ${{R}_{2}}$ be the equivalent resistance of series. Consider Combination of resistances $40\Omega ,\text{ 10}\Omega $. Consider Similarly ${{R}_{3}}\text{ for 20}\Omega ,\text{ 30}\Omega $
Then ${{R}_{1}},{{R}_{2}},{{R}_{3}}$ Is given as,
$\begin{align}
  & {{R}_{1}}=10+15=25\Omega \\
 & {{R}_{2}}=40+10=50\Omega \\
 & {{R}_{3}}=20+30=50\Omega \\
\end{align}$
So, the circuit will look like:

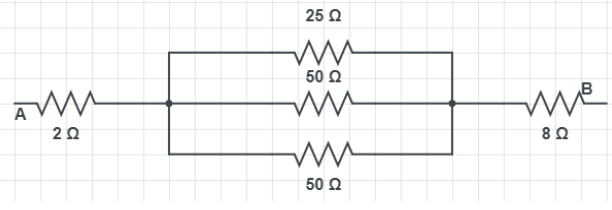
Now, these three resistances ${{R}_{1}},{{R}_{2}},{{R}_{3}}$ are parallel to each other i.e. they are connected in parallel. Therefore, equivalent resistance of parallel combination is given as,
$\dfrac{1}{{{R}_{p}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}$
Where, ${{R}_{P}}$ = equivalent resistance of parallel combination
$\begin{align}
  & \therefore \dfrac{1}{{{R}_{p}}}=\dfrac{1}{25}+\dfrac{1}{50}+\dfrac{1}{50} \\
 & =\dfrac{1}{25}+\dfrac{100}{2500} \\
 & =\dfrac{1}{25}+\dfrac{1}{25} \\
 & \Rightarrow \dfrac{1}{{{R}_{p}}}=\dfrac{2}{25} \\
 & \therefore {{R}_{P}}=\dfrac{25}{2}\Omega \\
\end{align}$
Now the circuit (simplified circuit) will look like:
So, the equivalent resistance ${{R}_{P}}$is inn series with both resistances $2\Omega \text{ and }8\Omega $
$\therefore {{R}_{eq}}={{R}_{p}}+2\Omega +8\Omega $
Where, ${{R}_{P}}$ = equivalent resistance (final) of series combination
$\therefore {{R}_{eq}}=2+\dfrac{25}{2}+8=10+\dfrac{25}{2}=\dfrac{45}{2}=22.5\Omega $

Hence equivalent resistance between points A and B is 22.5Ω.

Additional information:
Resistance in series: when a several number of resistances are connected in series then the equivalent resistance is equal to sum of individual resistances. If ${{R}_{1}},{{R}_{2}},{{R}_{3}}$ be the resistor connected in series than their equivalent resistance ${{R}_{3}}$ is given by,
${{R}_{s}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}$
Resistance in parallel: when several number of resistance are connected in parallel the reciprocal of the equivalent resistance is equal to the sum of reciprocal of individual resistances
$\dfrac{1}{{{R}_{p}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}$

Note:
When a number of resistors are connected in series then the current flowing through each of them will be the same when several numbers of resistors are connected in parallel then the potential difference across each of them will be always the same. Above question can be by simplifying the circuit or by reducing it in a simplified form by using concept or formula of resistance in series or resistance in parallel.