Question

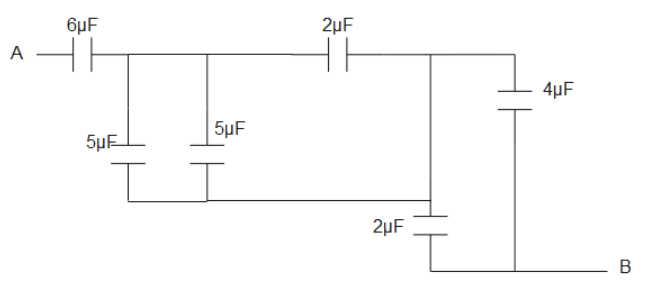
The equivalent capacitance between A and B in the circuit given below, is:

A. $2.4\mu F$
B. $4.9\mu F$
C. $3.6\mu F$
D. $5.4\mu F$

Answer 1

Hint: Capacitor is a device which is used to store the charge. The charge stored in the capacitor depends on the potential difference applied across them and also depends on the capacitance of the capacitor. We have different formulas to find out effective capacitance when they are connected in series or parallel.
Formula used:
$\eqalign{
  & \dfrac{1}{{{C_S}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}} + \dfrac{1}{{{C_4}}}{\text{ }}......... \cr
  & {C_P} = {C_1} + {C_2} + {C_3} + {C_4}{\text{ }}........... \cr} $

Complete answer:
Generally when there are more than one capacitors, we can connect them in series or we can connect them in parallel.
In case of series connection the current flowing through the circuit will be the same which means that the charge stored on the every capacitor will be the same as the charge is nothing but the current flowing in a given time.
In case of parallel connection the voltage across all the capacitors will be the same.
In series connection charge will be same and voltage will be divided across the capacitors whereas in parallel connection voltage will be same and charge will be divided across the capacitors.
Effective capacitance for capacitors in series connection is
$\dfrac{1}{{{C_S}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}} + \dfrac{1}{{{C_4}}}{\text{ }}.........$
Effective capacitance for capacitors in parallel connection is
${C_P} = {C_1} + {C_2} + {C_3} + {C_4}{\text{ }}...........$

In the above circuit 5 and 5 are in parallel so effective would be
$\eqalign{
  & {C_P} = {C_1} + {C_2} + {C_3} + {C_4}{\text{ }}........... \cr
  & \therefore {C_P} = 5 + 5 = 10\mu F \cr} $
Now 10 and upper branch 2 are in parallel so effective would be
$\eqalign{
  & {C_P} = {C_1} + {C_2} + {C_3} + {C_4}{\text{ }}........... \cr
  & \therefore {C_P} = 10 + 2 = 12\mu F \cr} $
Now 4 and remaining 2 are in parallel so their effective would be
$\eqalign{
  & {C_P} = {C_1} + {C_2} + {C_3} + {C_4}{\text{ }}........... \cr
  & \therefore {C_P} = 4 + 2 = 6\mu F \cr} $
So the final capacitances between A and B are 12 and 6 from above and 6 which is adjacent to A.
All these 3 capacitances are in series so effective would be
$\eqalign{
  & \dfrac{1}{{{C_S}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}} + \dfrac{1}{{{C_4}}}{\text{ }}......... \cr
  & \Rightarrow \dfrac{1}{{{C_S}}} = \dfrac{1}{6} + \dfrac{1}{6} + \dfrac{1}{{12}} \cr
  & \therefore {C_S} = \dfrac{{12 \times 3}}{{12 + 3}} = \dfrac{{36}}{{15}} = 2.4\mu F \cr} $

Hence option A is the answer.

Note:
The formulas which we have for the case of finding effective capacitance of parallel and series connection of capacitors will be exactly opposite to the case of finding effective resistance of parallel and series connection of resistors. If we know the voltage across AB we can find out the total charge passing through the system given as we had got the effective capacitance.