Question

The equilibrium constant ${K_P}$ for the reaction:

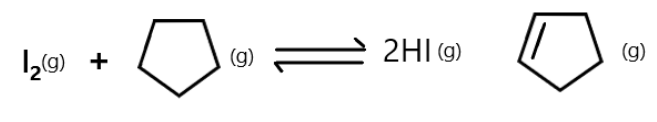
Varies with temperatures according to the equation:
${\log _{10}}({K_P}ba{r^{ - 1}}) = 7.55 - 4844{(T{K^{ - 1}})^{ - 1}}$
Calculate ${K_P},\Delta {G^o},\Delta {H^o}$ and $\Delta {S^o}$ at $1$ bar and ${400^\circ }C$.

Answer 1

Hint:As we know that Gibbs free energy is the energy that should be supplied to a system and only a small portion of it is converted to useful work which is our free energy, entropy is the randomness of the system and the enthalpy is the amount of heat supplied at constant pressure.

Complete answer:
We know that Gibbs free energy is the energy that should be supplied to a system and only a small portion of it is converted to useful work which is our free energy, entropy is the randomness of the system and the enthalpy is the amount of heat supplied at constant pressure and the equilibrium constant is that value where the reaction has no tendency to move forward or backward.
Now, We are given that the temperature is ${400^\circ }C$, we will first convert it into kelvin so we will get:
$400 + 273 = 673K$
Then we are provided with the equation:
${\log _{10}}({K_P}ba{r^{ - 1}}) = 7.55 - 4844{(T{K^{ - 1}})^{ - 1}}$
We will first solve this equation for finding out the equilibrium constant ${K_P}$ and after solving this equation we will get:
$\log {K_P} = 7.55 - \dfrac{{4844}}{{673}}$
$\Rightarrow \log {K_P} = 0.352$
$
\Rightarrow {K_P} = anti\log (0.352) \\
\Rightarrow {K_P} = 2.25
 $
Now we can use this value of equilibrium constant ${K_P}$to calculate the Gibbs free energy using the formula:
$\Delta {G^\circ } = - RT\;In\;{K_P}$
$\Rightarrow\Delta {G^\circ } = - 2.303 \times 8.314 \times 673 \times 0.352$
$= - 4535.8\;J$ or in terms of kilojoules it will be $ - 4.54\;kJ$.
Now, we will solve for change in enthalpy $\Delta {H^o}$using the formula:
$\Rightarrow\ln {K_P} = - \dfrac{{\Delta {H^\circ }}}{{RT}}$
\Rightarrow$2.303\;\log {K_P} = - \dfrac{{\Delta {H^\circ }}}{{673}}$
$
\Rightarrow \Delta {H^\circ } = 2.303 \times 0.352 \times 673 \times 8.314 \\
\Rightarrow \Delta {H^\circ } = 4.536\;kJ
 $
Therefore the value of change in enthalpy is $\Delta {H^\circ } = 4.536\;kJ$.
Now we can calculate the change in entropy using the formula:
$\Delta {G^\circ } = \Delta {H^\circ } - T\Delta {S^\circ }$
$ - 4.54 = 4.536 - 673 \times \Delta {S^\circ }$
$13.49\,Jmo{l^{ - 1}} = \Delta {S^\circ }$
Hence the value of change in entropy is $13.49Jmo{l^{ - 1}}$.

Therefore the values of ${K_P} = 2.25$, $\Delta {G^\circ } - 4.54\;kJ$, $\Delta {H^\circ } = 4.536\;kJ$ and $13.49Jmo{l^{ - 1}} = \Delta {S^\circ }$.

Note:
Always remember that for a reaction to be spontaneous, Gibbs free energy is always spontaneous when its value is present in negative, similarly change in enthalpy should also be negative and change in entropy should be always positive and for a non spontaneous reaction to occur, Gibbs free energy is always positive, change in enthalpy is also positive and change in entropy is always negative. At equilibrium all these dimensions are zero.