Question

The equations of the tangents to the ellipse $9{x^2} + 16{y^2} = 144$ from the point $\left( {2,3} \right)$ are:
(A) $y = 3,x = 5$
(B) $y = 3,x = 2$
(C) $x = 3,y = 2$
(D) $x + y = 5,y = 3$

Answer 1

Hint: In the given question, we are required to find the equations of the tangents to the ellipse whose equation is provided to us in the question from the point $\left( {2,3} \right)$. So, we first find the general equation of the line passing through the point $\left( {2,3} \right)$ and then apply the condition of tangency with the ellipse to get to the required answer.

Complete answer:
Firstly, we have the point $\left( {2,3} \right)$. So, we find the equation of the line passing through this point.
We know the slope intercept form as $y = mx + c$. So, we substitute x as $2$ and y as $3$.
Hence, we get,
$ \Rightarrow 3 = 2m + c$
Finding value of c in terms of m, we get,
$ \Rightarrow c = 3 - 2m$
So, we have the equation line passing through $\left( {2,3} \right)$ as $y = mx + \left( {3 - 2m} \right) - - - - - \left( 1 \right)$.
Now, we have the equation of the ellipse as $9{x^2} + 16{y^2} = 144$.
Dividing both sides by $144$, we have,
\[ \Rightarrow \dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{9} = 1\]
Now, we can see that the equation of the ellipse resembles with \[\dfrac{{{x^2}}}{a} + \dfrac{{{y^2}}}{b} = 1\], where a is greater than b.
We get ${a^2} = 16$ and ${b^2} = 9$
So, the value of a is $4$ and that of b is $3$.
Now, we know the condition of tangency of a line $y = mx + c$ with an ellipse \[\dfrac{{{x^2}}}{a} + \dfrac{{{y^2}}}{b} = 1\] is ${c^2} = {a^2}{m^2} + {b^2}$.
So, we get, ${\left( {3 - 2m} \right)^2} = 16{m^2} + 9$
Evaluating the whole square using algebraic identity ${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$, we get,
$ \Rightarrow 9 + 4{m^2} - 12m = 16{m^2} + 9$
Adding up like terms and solving for m, we get,
$ \Rightarrow 12{m^2} + 12m = 0$
$ \Rightarrow 12m\left( {m + 1} \right) = 0$
So, either $m = 0$ or $\left( {m + 1} \right) = 0$
$ \Rightarrow m = 0$ or $ \Rightarrow m = - 1$
So, the value of m is zero or $ - 1$.
Substituting the value of m as zero in equation $\left( 1 \right)$, we get,
$y = 0x + \left( {3 - 2 \times 0} \right)$
Simplifying calculations, we get,
$y = 3$
Now, substituting m as $ - 1$, we get,
$y = \left( { - 1} \right)x + \left( {3 - 2 \times \left( { - 1} \right)} \right)$
$ \Rightarrow y + x = 5$
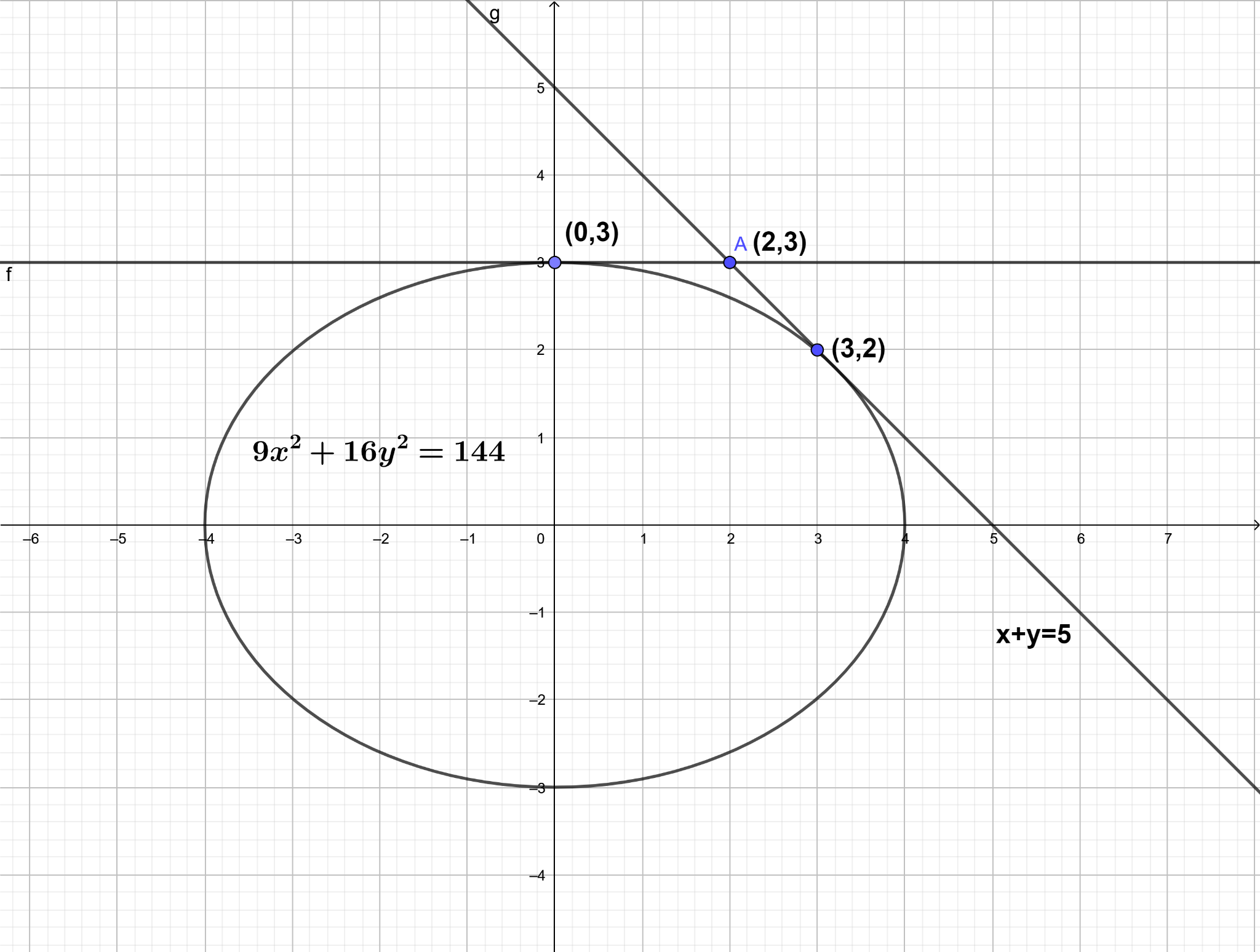
So, the equations of the tangents to the ellipse $9{x^2} + 16{y^2} = 144$ from the point $\left( {2,3} \right)$ are: $y + x = 5$ and $y = 3$.

Hence, option (D) is the correct answer.

Note:
The values of a and b in the equation of the ellipse \[\dfrac{{{x^2}}}{a} + \dfrac{{{y^2}}}{b} = 1\] represent the lengths of semi-major and semi-minor axes of an ellipse and hence the values cannot be negative. The condition of tangency for a line with ellipse \[\dfrac{{{x^2}}}{a} + \dfrac{{{y^2}}}{b} = 1\] is ${c^2} = {a^2}{m^2} + {b^2}$ where the equation of the line is $y = mx + c$.