Question

The equation of the parabola, whose vertex is \[\left( { - 1, - 2} \right)\] axis is vertical and which passes through the point \[\left( {3,6} \right)\] is
A. \[{x^2} + 2x - 2y - 3 = 0\]
B. \[2{x^2} = 3y\]
C. \[{x^2} - 2x + y + 3 = 0\]
D. None of these

Answer 1

Hint:Here in this question, we have to find the equation of the parabola of a given vertex. Given the parabola axis is vertical for vertical axis the equation of parabola at the origin is \[{x^2} = 4ay\] or at any vertex \[\left( {h,k} \right)\] the equation of parabola is \[{\left( {x - h} \right)^2} = 4a\left( {y - k} \right)\], where a be a value that can be find by using a point \[\left( {3,6} \right)\] and on further simplification we get the required solution.

Complete step by step answer:
A parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped.Consider the question: given the vertex of the parabola, whose axis is vertical and which passes through the point \[\left( {3,6} \right)\]. We have to find the equation of parabola? Since the given axis of the parabola is vertical, the equation of the parabola would be the form of \[{x^2} = 4ay\].

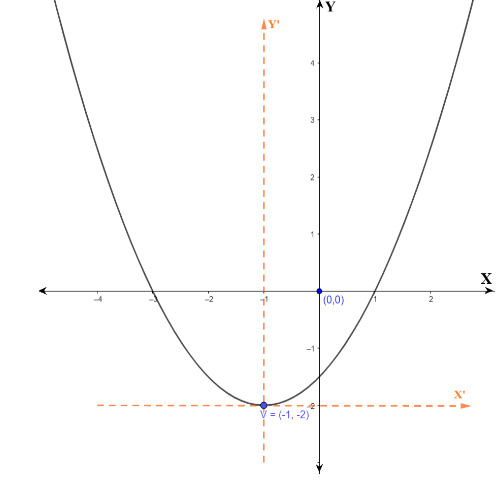
At any vertex \[\left( {h,k} \right)\] the equation will be \[{\left( {x - h} \right)^2} = 4a\left( {y - k} \right)\], then
The given vertex is \[\left( { - 1, - 2} \right)\] the equation will be
\[ \Rightarrow \,\,{\left( {x - \left( { - 1} \right)} \right)^2} = 4a\left( {y - \left( { - 2} \right)} \right)\]
On using sign convention, we have
\[ \Rightarrow \,\,{\left( {x + 1} \right)^2} = 4a\left( {y + 2} \right)\]-----(1)

Now find the value of ‘a’. Given the parabola passes through the point \[\left( {3,6} \right)\].
Substitute \[x = 3\] and \[y = 6\] value in equation (1), then we have
\[ \Rightarrow \,\,{\left( {3 + 1} \right)^2} = 4a\left( {6 + 2} \right)\]
\[ \Rightarrow \,\,{4^2} = 4a\left( 8 \right)\]
\[ \Rightarrow \,\,16 = 32a\]
\[ \Rightarrow \,\,32a = 16\]
Divide both side by 32
\[ \Rightarrow \,\,a = \dfrac{{16}}{{32}}\]
 Divide both numerator and denominator by 16, then we get
\[\therefore \,\,a = \dfrac{1}{2}\]

Substitute the value of a in equation (1), then
\[ \Rightarrow \,\,{\left( {x + 1} \right)^2} = 4\left( {\dfrac{1}{2}} \right)\left( {y + 2} \right)\]
On simplification, we have
\[ \Rightarrow \,\,{\left( {x + 1} \right)^2} = 2\left( {y + 2} \right)\]
Apply a algebraic identity: \[{\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab\], then
\[ \Rightarrow \,\,{x^2} + {1^2} + 2\left( x \right)\left( 1 \right) = 2y + 4\]
\[ \Rightarrow \,\,{x^2} + {1^2} + 2x = 2y + 4\]
Subtract \[\left( {2y + 4} \right)\] on both side, we have
\[ \Rightarrow \,\,{x^2} + 1 + 2x - \left( {2y + 4} \right) = 2y + 4 - \left( {2y + 4} \right)\]
\[ \Rightarrow \,\,{x^2} + 1 + 2x - 2y - 4 = 2y + 4 - 2y - 4\]
\[ \Rightarrow \,\,{x^2} + 1 + 2x - 2y - 4 = 0\]
On simplification, we get
\[ \therefore \,\,{x^2} + 2x - 2y - 3 = 0\]
Hence, the equation of parabola is \[{x^2} + 2x - 2y - 3 = 0\].

Therefore, option A is correct.

Note:There are two general standard equation of a parabola having vertex \[\left( {0,0} \right)\] is: if parabola is parallel to the y-axis or horizontal to the axis the standard equation of a parabola is \[{y^2} = 4ax\]similarly if parabola is parallel to the y-axis or vertical to the axis the standard equation of a parabola is \[{x^2} = 4ay\].