Question

The equation of the normal to the circle ${x^2} + {y^2} = 2x$ , which is parallel to the line $x + 2y = 3$ is
A.$x + 3y = 7$
B.$x + 2y = 1$
C.$x + 2y = 2$
D.$x + 2y = 5$

Answer 1

Hint: First we’ll find the coordinate of the center of the circle because we know that all the normals of the circle pass through its center and we have the line parallel to the normal required so we’ll get the slope of the normal as parallel lines have an equal slope.
Then we'll find the equation of the normal using the point-slope form of the line.

Complete step-by-step answer:
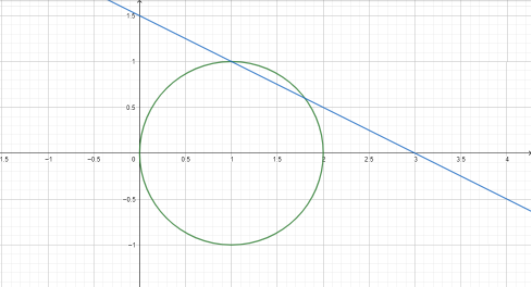
Given data: Equation of the circle
Line parallel to required line i.e. $x + 2y = 3$

If the equation of a circle is ${(x - a)^2} + {(y - b)^2} = {r^2}$
Then (a, b) is the center of the circle
On simplifying the equation of the given circle,
i.e. ${x^2} + {y^2} = 2x$
$ \Rightarrow {x^2} - 2x + {y^2} = 0$
Adding ${1^2}$ both the sides
$ \Rightarrow {x^2} - 2x + {1^2} + {y^2} = {1^2}$
Using ${a^2} + {b^2} - 2ab = {(a - b)^2}$
$ \Rightarrow {(x - 1)^2} + {(y - 0)^2} = {1^2}$
The Centre of the given circle is(1, 0)
We know that normal of a circle always passes through its center is given parallel to the line$x + 2y = 3$whose slope is $ - \dfrac{1}{2}$
Equation of a line passing through $({x_1},{y_1})$ and having slope (m) is given by
$(y - {y_1}) = m(x - {x_1})$
Therefore the equation of normal required is given by
$(y - 0) = - \dfrac{1}{2}(x - 1)$
On simplifying we get,
$ \Rightarrow 2y = - (x - 1)$
$ \Rightarrow 2y = - x + 1$
$ \Rightarrow 2y + x = 1$
Hence, The equation of the normal to the circle ${x^2} + {y^2} = 2x$ , which is parallel to the line $x + 2y = 3$ is $2y + x = 1$
Hence, Option(B) is correct.

Note: Alternative method to solve it is by,
On differentiating the equation of the circle with-respect-to ‘x’
i.e. $2x + 2y\dfrac{{dy}}{{dx}} = 2$
Dividing the whole equation by 2
$ \Rightarrow x + y\dfrac{{dy}}{{dx}} = 1$
$ \Rightarrow y\dfrac{{dy}}{{dx}} = 1 - x$
$ \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{1 - x}}{y}$
Therefore the slope of the tangent at any point of the circle will be $\dfrac{{1 - x}}{y}$
Since the product of slopes of two perpendicular lines is -1.
The slope of the normal at any point of the circle will be $\dfrac{y}{{x - 1}}$
Equating this with the slope of the line given parallel to this
i.e. $\dfrac{y}{{x - 1}} = - \dfrac{1}{2}$
$ \Rightarrow 2y = - (x - 1)$
$ \Rightarrow 2y + x = 1$
i.e. (B) $2y + x = 1$