Question

The equation of the line meeting the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\], two points at equal distances d from a point \[\left( {{x}_{1}},{{y}_{1}} \right)\] on the circumference is
(a) \[x{{x}_{1}}+y{{y}_{1}}-{{a}^{2}}+\dfrac{{{d}^{2}}}{2}=0\]
(b) \[x{{x}_{1}}-y{{y}_{1}}-{{a}^{2}}+\dfrac{{{d}^{2}}}{2}=0\]
(c) \[x{{x}_{1}}+y{{y}_{1}}+{{a}^{2}}-\dfrac{{{d}^{2}}}{2}=0\]
(d) \[x{{x}_{1}}+y{{y}_{1}}-{{a}^{2}}+\dfrac{{{d}^{2}}}{2}=0\]

Answer 1

Hint: Assume that line AB meets the circle, \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] at A and B. Assume the coordinates of A and B as \[\left( a\cos \theta ,a\sin \theta \right)\] and \[\left( a\cos \phi ,a\sin \phi \right)\] respectively. Find out the distance d using distance formula given by: - \[d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}\] and equate the two distances. Now, use the given point \[\left( {{x}_{1}},{{y}_{1}} \right)\] by substituting it in the equation of circle and eliminating the variable ‘\[\theta \]’ from the equation of line.

Complete step-by-step solution

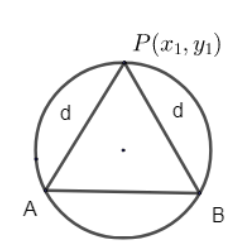
Let us assume from the above figure that line AB is the required line whose equation is to be found. We know that in the parametric form any point on the circle is assumed as \[\left( r\cos \theta,r\sin \theta \right)\], where ‘r’ is the radius of the circle.
Here, the equation of the circle, \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\]. So, radius of the circle is ‘a’. Therefore, assuming point A and B as \[\left( a\cos \theta ,a\sin \theta \right)\] and \[\left( a\cos \phi ,a\sin \phi \right)\] respectively.
We have been given that the distance of point P from A and B are equal.
\[\Rightarrow \] PA = PB.
Using distance formula: - \[d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}\], we get,
\[\Rightarrow \sqrt{{{\left( {{x}_{1}}-a\cos \theta \right)}^{2}}+{{\left( {{y}_{1}}-a\sin \theta \right)}^{2}}}=\sqrt{{{\left( {{x}_{1}}-a\cos \phi \right)}^{2}}+{{\left( {{y}_{1}}-a\sin \phi \right)}^{2}}}\]
On squaring both sides, we get,
\[\begin{align}
  & \Rightarrow {{\left( {{x}_{1}}-a\cos \theta \right)}^{2}}+{{\left( {{y}_{1}}-a\sin \theta \right)}^{2}}={{\left( {{x}_{1}}-a\cos \phi \right)}^{2}}+{{\left( {{y}_{1}}-a\sin \phi \right)}^{2}} \\
 & \Rightarrow \left( x_{1}^{2}+{{a}^{2}}{{\cos }^{2}}\theta -2a{{x}_{1}}\cos \theta \right)+\left( y_{1}^{2}+{{a}^{2}}{{\sin }^{2}}\theta -2a{{y}_{1}}\sin \theta \right) \\
 & \Rightarrow \left( x_{1}^{2}+{{a}^{2}}{{\cos }^{2}}\phi -2a{{x}_{1}}\cos \phi \right)+\left( y_{1}^{2}+{{a}^{2}}{{\sin }^{2}}\phi -2a{{y}_{1}}\sin \phi \right) \\
\end{align}\]
Cancelling the common terms and using the identity: - \[{{\cos }^{2}}x+{{\sin }^{2}}=1\], we get,
\[\begin{align}
  & \Rightarrow -2a{{x}_{1}}\cos \theta -2a{{y}_{1}}\sin \theta =-2a{{x}_{1}}\cos \phi -2a{{y}_{1}}\sin \phi \\
 & \Rightarrow -{{x}_{1}}\cos \theta -{{y}_{1}}\sin \theta =-{{x}_{1}}\cos \phi -{{y}_{1}}\sin \phi \\
 & \Rightarrow {{x}_{1}}\left( \cos \theta -\cos \phi \right)=-{{y}_{1}}\left( \sin \theta -\sin \phi \right) \\
\end{align}\]
\[\Rightarrow \left( \dfrac{\sin \theta -\sin \phi }{\cos \theta -\cos \phi } \right)=\dfrac{-{{x}_{1}}}{{{y}_{1}}}\] ------- (1)
Now, earlier we have calculated,
\[\Rightarrow d=\sqrt{{{\left( {{x}_{1}}-a\cos \theta \right)}^{2}}+{{\left( {{y}_{1}}-a\sin \theta \right)}^{2}}}\]
On squaring both sides, we get,
\[\Rightarrow {{d}^{2}}=x_{1}^{2}+{{a}^{2}}{{\cos }^{2}}\theta -2a{{x}_{1}}\cos \theta +y_{1}^{2}+{{a}^{2}}{{\sin }^{2}}\theta -2a{{y}_{1}}\sin \theta \]
\[\Rightarrow {{d}^{2}}=x_{1}^{2}+y_{1}^{2}+{{a}^{2}}-2a\left( {{x}_{1}}\cos \theta +{{y}_{1}}\sin \theta \right)\] -------- (ii)
Since, point P \[\left( {{x}_{1}},{{y}_{1}} \right)\] lies on the circle, therefore it will satisfy the equation of the circle.
\[\Rightarrow x_{1}^{2}+y_{1}^{2}={{a}^{2}}\]
Substituting this value in equation (ii), we get,
\[\Rightarrow {{d}^{2}}=2{{a}^{2}}-2a\left( {{x}_{1}}\cos \theta +{{y}_{1}}\sin \theta \right)\] ------ (iii)
Now, we know that equation of a line with points (a, b) and (c, d) is given as: -
\[\Rightarrow \left( y-b \right)=\left( \dfrac{b-d}{a-c} \right)\left( x-a \right)\]
So, equation of the line AB with points A \[\left( a\cos \theta ,a\sin \theta \right)\] and B \[\left( a\cos \phi ,a\sin \phi \right)\] can be given as: -
\[\begin{align}
  & \Rightarrow \left( y-a\sin \theta \right)=\left( \dfrac{a\sin \theta -a\sin \phi }{a\cos \theta -a\cos \phi } \right)\left( x-a\cos \theta \right) \\
 & \Rightarrow \left( y-a\sin \theta \right)=\left( \dfrac{\sin \theta -\sin \phi }{\cos \theta -\cos \phi } \right)\left( x-a\cos \theta \right) \\
\end{align}\]
Using equation (i), we get,
\[\Rightarrow \left( y-a\sin \theta \right)=\dfrac{-{{x}_{1}}}{{{y}_{1}}}\left( x-a\cos \theta \right)\]
By cross – multiplication we get,
\[\begin{align}
  & \Rightarrow y{{y}_{1}}-a{{y}_{1}}\sin \theta =-x{{x}_{1}}+a{{x}_{1}}\cos \theta \\
 & \Rightarrow y{{y}_{1}}+x{{x}_{1}}=a\left( {{y}_{1}}\sin \theta +{{x}_{1}}\cos \theta \right) \\
\end{align}\]
Using equation (iii), we get,
\[\begin{align}
  & \Rightarrow y{{y}_{1}}+x{{x}_{1}}=\dfrac{2{{a}^{2}}-{{d}^{2}}}{2} \\
 & \Rightarrow y{{y}_{1}}+x{{x}_{1}}={{a}^{2}}-\dfrac{{{d}^{2}}}{2} \\
 & \Rightarrow y{{y}_{1}}+x{{x}_{1}}-{{a}^{2}}+\dfrac{{{d}^{2}}}{2}=0 \\
\end{align}\]
Hence, option (a) is the correct answer.

Note: It is important to note that we have assumed the points A and B as parametric form. This is done to make our calculation easy. If any random variable is selected as these points then it will become too confusing and the chances of making mistakes will be more.