
The equation of the line making an angle \[{60^0}\] with x-axis and y-intercept $\dfrac{{ - 2}}{5}$ is:
Answer
570k+ views
Hint: The general equation of a straight line is \[y = mx + c\] , where \[m\] is the slope or the gradient, \[c\] is the y-intercept. In this question the angle which the line is making with the x-axis and the y-intercept is given so we will first find the slope of the line using the given angle and then we will substitute these values in the general equation of a straight line to find the equation of the straight line.
Complete step-by-step answer:
The y-intercept of the line is given as, \[c = - \dfrac{2}{5}\]
The line is making an angle of \[\theta = {60^ \circ }\] with the x-axis so the slope of the line which is given by the formula \[m = \tan \theta \] will be
\[m = \tan {60^ \circ } = \sqrt 3 {\text{ }}\left( {\because \tan {{60}^ \circ } = \sqrt 3 } \right)\]
So, the slope of the line is given as \[m = \sqrt 3 \]
Now, we know the general equation of a straight line is \[y = mx + c\] , so we will substitute the values of the slope and the y-intercept in the equation, hence the equation of the straight line will be
\[
y = \left( {\sqrt 3 } \right)x - \dfrac{2}{5} \\
\Rightarrow y = \sqrt 3 x - \dfrac{2}{5} \;
\]
Therefore, the required equation of the line whose slope is \[m = \sqrt 3 \] and the y-intercept \[c = - \dfrac{2}{5}\] is
\[y = \sqrt 3 x - \dfrac{2}{5}\]
So, the correct answer is “ \[y = \sqrt 3 x - \dfrac{2}{5}\] ”.
Note: Here, the y-intercept of the line is \[c = - \dfrac{2}{5}\] , the y-intercept means that the straight line cuts the y-axis at the point \[ - \dfrac{2}{5}\] which is in the negative side of the y-axis on an x-y graph plane and the line will move in the positive x-axis direction since the slope of the line is positive . We can plot the graph as
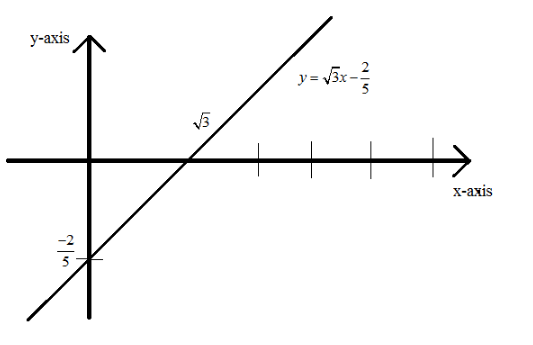
Complete step-by-step answer:
The y-intercept of the line is given as, \[c = - \dfrac{2}{5}\]
The line is making an angle of \[\theta = {60^ \circ }\] with the x-axis so the slope of the line which is given by the formula \[m = \tan \theta \] will be
\[m = \tan {60^ \circ } = \sqrt 3 {\text{ }}\left( {\because \tan {{60}^ \circ } = \sqrt 3 } \right)\]
So, the slope of the line is given as \[m = \sqrt 3 \]
Now, we know the general equation of a straight line is \[y = mx + c\] , so we will substitute the values of the slope and the y-intercept in the equation, hence the equation of the straight line will be
\[
y = \left( {\sqrt 3 } \right)x - \dfrac{2}{5} \\
\Rightarrow y = \sqrt 3 x - \dfrac{2}{5} \;
\]
Therefore, the required equation of the line whose slope is \[m = \sqrt 3 \] and the y-intercept \[c = - \dfrac{2}{5}\] is
\[y = \sqrt 3 x - \dfrac{2}{5}\]
So, the correct answer is “ \[y = \sqrt 3 x - \dfrac{2}{5}\] ”.
Note: Here, the y-intercept of the line is \[c = - \dfrac{2}{5}\] , the y-intercept means that the straight line cuts the y-axis at the point \[ - \dfrac{2}{5}\] which is in the negative side of the y-axis on an x-y graph plane and the line will move in the positive x-axis direction since the slope of the line is positive . We can plot the graph as
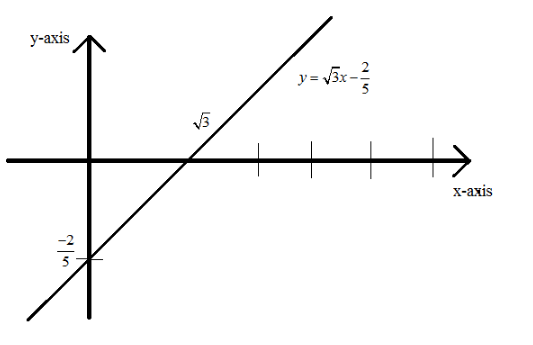
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




