
The equation of the circle which touches $x-axis$ at $\left( 3,0 \right)$ and passes through $\left( 1,4 \right)$ is given by
(a) ${{x}^{2}}+{{y}^{2}}-6x-5y+9=0$
(b) ${{x}^{2}}+{{y}^{2}}+6x+5y-9=0$
(c) ${{x}^{2}}+{{y}^{2}}-6x+5y-9=0$
(d) ${{x}^{2}}+{{y}^{2}}+6x-5y+9=0$
Answer
611.4k+ views
Hint: From the equation of circle, find the $x-\text{intercept}$ by putting $y=0$. Substitute the values in the equation of the circle and put $\left( x,y \right)=\left( 3,0 \right)\ and\ \left( 1,4 \right)$ as it passes through the circle and get the value of the centres of the circle.
Complete step by step answer:
We know that equation of the circle,
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0.......................\left( 1 \right)$
Here, the centre of circle $=\left( -g,-f \right)$
We need to find the $x$- intercept of the circle.
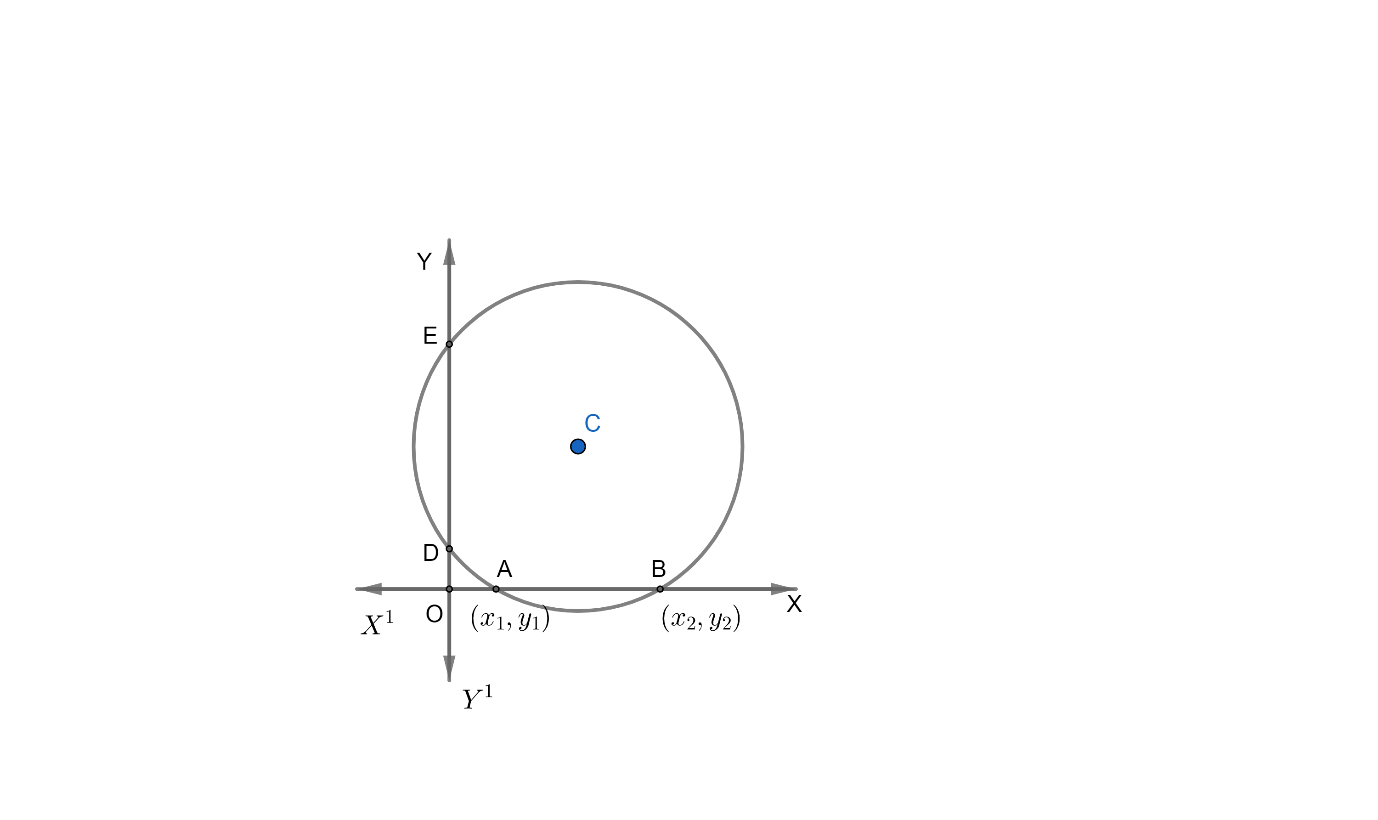
Consider the figure drawn.
Let $AB$ be the intercept made by the given circle on $x-axis$.
Since on $x-axis,y=0$ .
$\therefore x$- coordinate of the points
$A$ and $B$are the root of the equation ${{x}^{2}}+2gx+c=0.......................\left( 2 \right)$
$\because $ Substituting $y=0$ in equation (1) to obtain equation (2)
Let ${{x}_{1}}\text{ and }{{x}_{2}}$ be the x-coordinates of points $A\text{ and }B$ respectively
Then, ${{x}_{1}}\text{ and }{{x}_{2}}$also the roots of the equation ${{x}^{2}}+2gx+c=0$
$\begin{align}
& \therefore {{x}_{1}}+{{x}_{2}}=-2g \\
& {{x}_{1}}.{{x}_{2}}=c \\
& \because Where,\text{ }{{x}_{1}}=-g,{{x}_{2}}=-g \\
\end{align}$
X-coordinates
Clearly the intercept on $x-axis=AB$
$={{x}_{2}}-{{x}_{1}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}}$
We know $\left( {{a}^{2}}-{{b}^{2}} \right)=\left( a-b \right)\left( a+b \right)\text{ or }\left( {{a}^{2}}-{{b}^{2}} \right)={{\left( a+b \right)}^{2}}-4ab$
$\begin{align}
& \sqrt{{{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-4{{x}_{1}}{{x}_{2}}} \\
& =\sqrt{{{\left( -2g \right)}^{2}}-4c} \\
& =\sqrt{4{{g}^{2}}-4c} \\
& =\sqrt{4\left( {{g}^{2}}-c \right)} \\
& =2\sqrt{{{g}^{2}}-c} \\
\end{align}$
$\therefore $We got the $x-$ intercept made by circle on the $x-axis$
\[=2\sqrt{{{g}^{2}}-c}.............\left( 3 \right)\]
Now, the circle touches $x-axis$
$\begin{align}
& 2\sqrt{{{g}^{2}}-c}=0 \\
& \therefore c={{g}^{2}}.............\left( 4 \right) \\
\end{align}$
Substitute the value of equation (4) in equation (1)
${{x}^{2}}+{{y}^{2}}+2gx+2fy+{{g}^{2}}=0................\left( 5 \right)$
Given that the circle passes through $\left( 3,0 \right)$ and $\left( 1,4 \right)$
Consider point $\left( x,y \right)=\left( 3,0 \right)$ and substitute in equation (5)
$\therefore {{3}^{2}}+{{0}^{2}}+2g\times 3+0+{{g}^{2}}=0$
$\Rightarrow 9+6g+{{g}^{2}}=0$
Consider the quadratic equation ${{g}^{2}}+6g+9=0.........\left( 6 \right)$
By using the quadratic formula, we can solve this equation (6)
It is of the form $a{{x}^{2}}+bx+c=0$
And the equation we got ${{g}^{2}}+6g+9=0$
$\left[i.e.,x=g \right]$
From the equation we get the values of $a,b,c$ as
$a=1,b=6,c=9$
Put the values in the quadratic formula to obtain the roots
$\begin{align}
& \dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a} \\
& =\dfrac{-6\pm \sqrt{36-4\times 1\times 9}}{2\times 1} \\
& =\dfrac{-6\pm \sqrt{36-36}}{2} \\
& =\dfrac{-6\pm 0}{2}=\dfrac{-6}{2}=-3 \\
\end{align}$
$\therefore g=-3$
By substituting $\left( x,y \right)=\left( 1,4 \right)$ in equation (5)
${{x}^{2}}+{{y}^{2}}+2gx+2fy+{{g}^{2}}=0$
$\begin{align}
& {{1}^{1}}+{{4}^{2}}+2\times \left( -3 \right)\times 1+2f\times 4+{{\left( -3 \right)}^{2}}=0 \\
& 1+16-6+8f+9=0 \\
& \Rightarrow 20+8f=0 \\
& \therefore f=\dfrac{-5}{2} \\
\end{align}$
Hence the equation of the circle become,
$\begin{align}
& {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 \\
& {{x}^{2}}+{{y}^{2}}+2\left( -3 \right)x+2\left( \dfrac{-5}{2} \right)y+9=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}-6x-5y+9=0 \\
\end{align}$
Hence the correct answer is option (a).
Note: (i) In a question like you should be careful with the calculation part as not to mix up the sign.
The solutions options are similar and if you get the sign wrong. You might get the wrong answer and thus choose the wrong solution.
(ii) The intercept is the crossing point, and the $x$ - intercept of a graph refers to the point at which the equation crosses the $x-axis$ of the coordinate plane.
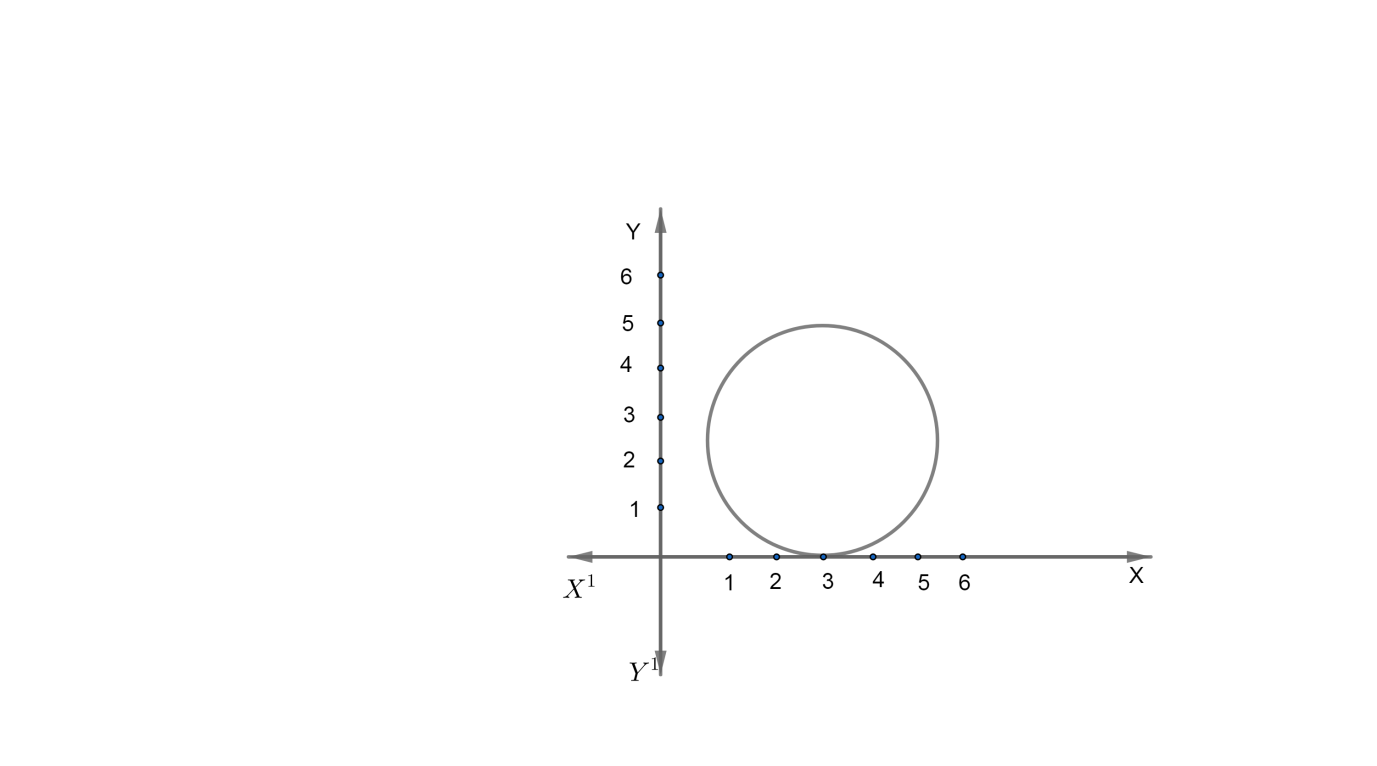
Complete step by step answer:
We know that equation of the circle,
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0.......................\left( 1 \right)$
Here, the centre of circle $=\left( -g,-f \right)$
We need to find the $x$- intercept of the circle.

Consider the figure drawn.
Let $AB$ be the intercept made by the given circle on $x-axis$.
Since on $x-axis,y=0$ .
$\therefore x$- coordinate of the points
$A$ and $B$are the root of the equation ${{x}^{2}}+2gx+c=0.......................\left( 2 \right)$
$\because $ Substituting $y=0$ in equation (1) to obtain equation (2)
Let ${{x}_{1}}\text{ and }{{x}_{2}}$ be the x-coordinates of points $A\text{ and }B$ respectively
Then, ${{x}_{1}}\text{ and }{{x}_{2}}$also the roots of the equation ${{x}^{2}}+2gx+c=0$
$\begin{align}
& \therefore {{x}_{1}}+{{x}_{2}}=-2g \\
& {{x}_{1}}.{{x}_{2}}=c \\
& \because Where,\text{ }{{x}_{1}}=-g,{{x}_{2}}=-g \\
\end{align}$
X-coordinates
Clearly the intercept on $x-axis=AB$
$={{x}_{2}}-{{x}_{1}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}}$
We know $\left( {{a}^{2}}-{{b}^{2}} \right)=\left( a-b \right)\left( a+b \right)\text{ or }\left( {{a}^{2}}-{{b}^{2}} \right)={{\left( a+b \right)}^{2}}-4ab$
$\begin{align}
& \sqrt{{{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-4{{x}_{1}}{{x}_{2}}} \\
& =\sqrt{{{\left( -2g \right)}^{2}}-4c} \\
& =\sqrt{4{{g}^{2}}-4c} \\
& =\sqrt{4\left( {{g}^{2}}-c \right)} \\
& =2\sqrt{{{g}^{2}}-c} \\
\end{align}$
$\therefore $We got the $x-$ intercept made by circle on the $x-axis$
\[=2\sqrt{{{g}^{2}}-c}.............\left( 3 \right)\]
Now, the circle touches $x-axis$
$\begin{align}
& 2\sqrt{{{g}^{2}}-c}=0 \\
& \therefore c={{g}^{2}}.............\left( 4 \right) \\
\end{align}$
Substitute the value of equation (4) in equation (1)
${{x}^{2}}+{{y}^{2}}+2gx+2fy+{{g}^{2}}=0................\left( 5 \right)$
Given that the circle passes through $\left( 3,0 \right)$ and $\left( 1,4 \right)$
Consider point $\left( x,y \right)=\left( 3,0 \right)$ and substitute in equation (5)
$\therefore {{3}^{2}}+{{0}^{2}}+2g\times 3+0+{{g}^{2}}=0$
$\Rightarrow 9+6g+{{g}^{2}}=0$
Consider the quadratic equation ${{g}^{2}}+6g+9=0.........\left( 6 \right)$
By using the quadratic formula, we can solve this equation (6)
It is of the form $a{{x}^{2}}+bx+c=0$
And the equation we got ${{g}^{2}}+6g+9=0$
$\left[i.e.,x=g \right]$
From the equation we get the values of $a,b,c$ as
$a=1,b=6,c=9$
Put the values in the quadratic formula to obtain the roots
$\begin{align}
& \dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a} \\
& =\dfrac{-6\pm \sqrt{36-4\times 1\times 9}}{2\times 1} \\
& =\dfrac{-6\pm \sqrt{36-36}}{2} \\
& =\dfrac{-6\pm 0}{2}=\dfrac{-6}{2}=-3 \\
\end{align}$
$\therefore g=-3$
By substituting $\left( x,y \right)=\left( 1,4 \right)$ in equation (5)
${{x}^{2}}+{{y}^{2}}+2gx+2fy+{{g}^{2}}=0$
$\begin{align}
& {{1}^{1}}+{{4}^{2}}+2\times \left( -3 \right)\times 1+2f\times 4+{{\left( -3 \right)}^{2}}=0 \\
& 1+16-6+8f+9=0 \\
& \Rightarrow 20+8f=0 \\
& \therefore f=\dfrac{-5}{2} \\
\end{align}$
Hence the equation of the circle become,
$\begin{align}
& {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 \\
& {{x}^{2}}+{{y}^{2}}+2\left( -3 \right)x+2\left( \dfrac{-5}{2} \right)y+9=0 \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}-6x-5y+9=0 \\
\end{align}$
Hence the correct answer is option (a).
Note: (i) In a question like you should be careful with the calculation part as not to mix up the sign.
The solutions options are similar and if you get the sign wrong. You might get the wrong answer and thus choose the wrong solution.
(ii) The intercept is the crossing point, and the $x$ - intercept of a graph refers to the point at which the equation crosses the $x-axis$ of the coordinate plane.

Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




