Question

The equation of the circle which passes through the origin and cuts off chords of length 2 on the lines \[x=y\] and \[x=-y\] is
A.\[{{x}^{2}}+{{y}^{2}}\pm 2\sqrt{2}y=0,{{x}^{2}}+{{y}^{2}}\pm 2\sqrt{2}x=0\]
B.\[{{x}^{2}}+{{y}^{2}}\pm 3\sqrt{3}y=0,{{x}^{2}}+{{y}^{2}}\pm 3\sqrt{3}x=0\]
C.\[{{x}^{2}}+{{y}^{2}}\pm 4\sqrt{2}x=0,{{x}^{2}}+{{y}^{2}}\pm 4\sqrt{2}y=0\]
D.\[{{x}^{2}}+{{y}^{2}}\pm 4\sqrt{2}x=0,{{x}^{2}}+{{y}^{2}}\pm 4\sqrt{3}y=0\]

Answer 1

Hint: Assume the equation of the circle \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] . Since the given circle is passing through the origin, so the coordinates of origin should satisfy the equation of the circle. After satisfying we get the value of c which is equal to 0. We have two chords whose equations are \[x=y\] and \[x=-y\] . The equation of the chords should satisfy the equation of the circle. After satisfying we will get the coordinates of the points where the chords intersect the circle. Using distance formula get the distance of the chords and make it equal to 2. Now, we get two equations and we have two variables that are g and f. Solve for g and f and get the values of g and f.

Complete step-by-step answer:
First of all, let us assume the equation of the circle \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] ………………………..(1)
Since the given circle is passing through the origin, so the coordinates of origin should satisfy the equation of the circle.
Putting the coordinates of the origin \[(0,0)\] in the equation of the circle, we get
\[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\]
\[\begin{align}
  & \Rightarrow {{0}^{2}}+{{0}^{2}}+2g0+2f0+c=0 \\
 & \Rightarrow 0+0+0+0+c=0 \\
\end{align}\]
\[\Rightarrow c=0\] ………………….(2)
The chord \[x=y\] intersects the circle, so it must satisfy the equation of the circle.
Putting, \[x=y\] in the equation of the circle \[({{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0)\] , we get
\[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\]
\[{{x}^{2}}+{{x}^{2}}+2gx+2fx+c=0\]
Putting the value of c from equation (2) in the above equation, we get
\[{{x}^{2}}+{{x}^{2}}+2gx+2fx+0=0\]
\[\begin{align}
  & \Rightarrow 2{{x}^{2}}+2gx+2fx=0 \\
 & \Rightarrow 2x\left( x+g+f \right)=0 \\
\end{align}\]
\[x=0\] or \[x+g+f=0\Rightarrow x=-(g+f)\]
Putting, \[x=0\] in the equation \[x=y\] , we get
\[y=0\] .
Putting, \[x=-(g+f)\]in the equation \[x=y\] , we get
\[y=-(g+f)\] .
We have got the points of intersection where the chord \[x=y\] meets the circle and the points are
\[(0,0)\] and \[\left( -(g+f),-(g+f) \right)\] .
The chord \[x=-y\] intersects the circle, so it must satisfy the equation of the circle.
Putting, \[x=-y\] in the equation of the circle \[({{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0)\] , we get
\[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\]
\[{{x}^{2}}+{{(-x)}^{2}}+2gx+2f(-x)+c=0\]
Putting the value of c from equation (2) in the above equation, we get
\[{{x}^{2}}+{{x}^{2}}+2gx-2fx+0=0\]
\[\begin{align}
  & \Rightarrow 2{{x}^{2}}+2gx-2fx=0 \\
 & \Rightarrow 2x\left( x+g-f \right)=0 \\
\end{align}\]
\[x=0\] or \[x+g-f=0\Rightarrow x=(f-g)\]
Putting, \[x=0\] in the equation \[x=-y\] , we get
\[y=0\] .
Putting, \[x=(f-g)\]in the equation \[x=-y\] , we get
\[y=(g-f)\] .
We have got the points of intersection where the chord \[x=-y\] meets the circle and the points are
\[(0,0)\] and \[\left( f-g,g-f \right)\] .

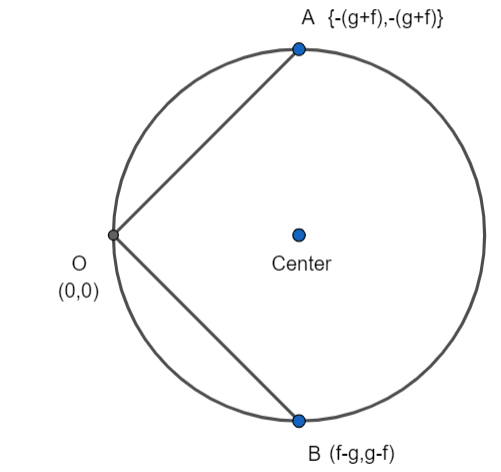
From the figure, we can see that the length of the chords is OA and AB and it is given that the length of the chords is 2.
OA = OB = 2 …………………….(3)
Using distance formula,
\[\begin{align}
  & OA=\sqrt{{{\left\{ 0-\left( -(g+f) \right) \right\}}^{2}}+{{\left\{ 0-\left( -(g+f) \right) \right\}}^{2}}} \\
 & OA=\sqrt{{{\left( g+f \right)}^{2}}+{{\left( g+f \right)}^{2}}} \\
\end{align}\]
Putting the value of OA=2 and squaring both sides in the above equation, we get
\[\begin{align}
  & \Rightarrow O{{A}^{2}}=2{{\left( g+f \right)}^{2}} \\
 & \Rightarrow {{2}^{2}}=2{{\left( g+f \right)}^{2}} \\
 & \Rightarrow 4=2{{\left( g+f \right)}^{2}} \\
 & \Rightarrow 2={{\left( g+f \right)}^{2}} \\
\end{align}\]
\[\Rightarrow \pm \sqrt{2}=(g+f)\] ……………………(4)
Using distance formula,
\[OB=\sqrt{{{\left\{ 0-\left( f-g \right) \right\}}^{2}}+{{\left\{ 0-\left( g-f \right) \right\}}^{2}}}\]
\[OB=\sqrt{{{(-1\left( g-f \right))}^{2}}+{{\left( g-f \right)}^{2}}}\] …………………….(5)
Or, \[OB=\sqrt{{{\left( f-g \right)}^{2}}+{{(-1\left( f-g \right))}^{2}}}\] ……………………..(6)
Putting the value of OB=2 and squaring both sides in equation (5), we get
\[\begin{align}
  & \Rightarrow O{{B}^{2}}=2{{\left( g-f \right)}^{2}} \\
 & \Rightarrow {{2}^{2}}=2{{\left( g-f \right)}^{2}} \\
 & \Rightarrow 4=2{{\left( g-f \right)}^{2}} \\
 & \Rightarrow 2={{\left( g-f \right)}^{2}} \\
\end{align}\]
\[\Rightarrow \pm \sqrt{2}=(g-f)\] ……………………(7)
Similarly, putting the value of OB=2 and squaring both sides in equation (6), we get
\[\begin{align}
  & \Rightarrow O{{B}^{2}}=2{{\left( f-g \right)}^{2}} \\
 & \Rightarrow {{2}^{2}}=2{{\left( f-g \right)}^{2}} \\
 & \Rightarrow 4=2{{\left( f-g \right)}^{2}} \\
 & \Rightarrow 2={{\left( f-g \right)}^{2}} \\
\end{align}\]
\[\Rightarrow \pm \sqrt{2}=(f-g)\] ………………………….(8)
On adding equation (4) and equation (7), we get
\[\pm \sqrt{2}=(g+f)\]
\[\pm \sqrt{2}=(g-f)\]
\[\begin{align}
  & \pm 2\sqrt{2}=2g \\
 & \Rightarrow \pm \sqrt{2}=g \\
\end{align}\]
Putting the value of g in equation (4), we get
\[\begin{align}
  & \pm \sqrt{2}=(\pm \sqrt{2}+f) \\
 & \Rightarrow 0=f \\
\end{align}\]
Here, the values of g and f are \[\pm 2\] and 0 respectively.
Now, putting the values of c, g and f in equation(1), we get
\[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\]
\[\begin{align}
  & \Rightarrow {{x}^{2}}+{{y}^{2}}+2\left( \pm \sqrt{2} \right)x+2.0.y+0=0 \\
 & \Rightarrow {{x}^{2}}+{{y}^{2}}\pm 2\sqrt{2}x=0 \\
\end{align}\]
On adding equation (4) and equation (8), we get
\[\pm \sqrt{2}=(g+f)\]
\[\pm \sqrt{2}=(f-g)\]
\[\begin{align}
  & \pm 2\sqrt{2}=2f \\
 & \Rightarrow \pm \sqrt{2}=f \\
\end{align}\]
Putting the value of f in equation (4), we get
\[\begin{align}
  & \pm \sqrt{2}=(\pm \sqrt{2}+g) \\
 & \Rightarrow 0=g \\
\end{align}\]
Here, the values of g and f are 0 and \[\pm 2\] respectively.
Now, putting the values of c, g and f in equation(1), we get
\[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\]
\[\begin{align}
  & \Rightarrow {{x}^{2}}+{{y}^{2}}++2.0.x+2\left( \pm \sqrt{2} \right)y+0=0 \\
 & \Rightarrow {{x}^{2}}+{{y}^{2}}\pm 2\sqrt{2}y=0 \\
\end{align}\]
The equation of the circle is \[{{x}^{2}}+{{y}^{2}}\pm 2\sqrt{2}y=0\] , \[{{x}^{2}}+{{y}^{2}}\pm 2\sqrt{2}x=0\] .
Hence, the correct option is option (A).


Note: This question involves a little bit of calculation. So, we have to be attentive to the calculations involved. Also, in this question, one may miss the point that \[OB=\sqrt{{{\left\{ 0-\left( f-g \right) \right\}}^{2}}+{{\left\{ 0-\left( g-f \right) \right\}}^{2}}}\] may also be written as \[OB=\sqrt{{{(-1\left( g-f \right))}^{2}}+{{\left( g-f \right)}^{2}}}\] or \[OB=\sqrt{{{\left( f-g \right)}^{2}}+{{(-1\left( f-g \right))}^{2}}}\] . Here, we have to solve both \[OB=\sqrt{{{(-1\left( g-f \right))}^{2}}+{{\left( g-f \right)}^{2}}}\] and \[OB=\sqrt{{{\left( f-g \right)}^{2}}+{{(-1\left( f-g \right))}^{2}}}\] . If we focus on only one of these two, then we will get only one equation of the circle. But, we can see that every option contains two equations of the circle. So, we require two equations of the circle. Therefore, we have to solve both \[OB=\sqrt{{{(-1\left( g-f \right))}^{2}}+{{\left( g-f \right)}^{2}}}\] and \[OB=\sqrt{{{\left( f-g \right)}^{2}}+{{(-1\left( f-g \right))}^{2}}}\] .