Question

The equation of incircle of the triangle formed by the axes and the line $4x + 3y = 6$
A.${x^2} + {y^2} - 6x - 6y = 0$
B.\[4\left( {{x^2} + {y^2} - x - y} \right) + 1 = 0\]
C.\[4\left( {{x^2} + {y^2} + x + y} \right) + 1 = 0\]
D.None of these

Answer 1

Hint: First we calculate the end point of the coordinate axes by putting $x = y = 0$ in the given equation, so we get the coordinates. Then we calculate the radius of the inscribed circle by using the formula. After that we get the equation of radius of circle and then solve the equation we get the value of radius.
Formula: $\dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$

Complete step-by-step answer:
Given equation is $4x + 3y = 6$
Consider the diagram

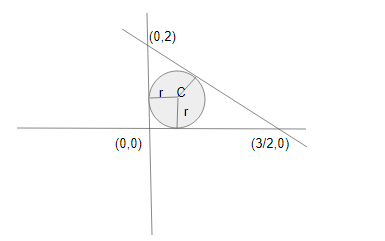
Find the endpoints of the coordinate axes:
Put
 $
  x = 0 \\
  0 + 3y = 6 \\
   \Rightarrow 3y = 6 \\
   \Rightarrow y = 2 \\
$
Now put
$
  y = 0 \\
  4x + 0 = 6 \\
   \Rightarrow 4x = 6 \\
   \Rightarrow x = \dfrac{3}{2} \\
$
Now we get three coordinate axes
$
  \left( {0,0} \right) \\
  \left( {0,2} \right) \\
  \left( {\dfrac{3}{2},0} \right) \\
$
Now the coordinate of circle centre is C$\left( {r,r} \right)$
\[
  \dfrac{{\left| {4r + 3r - 6} \right|}}{5} = r \\
   \Rightarrow {\left( {7r - 6} \right)^2} = 25{r^2} \\
   \Rightarrow 49{r^2} - 84r + 36 = 25{r^2} \\
   \Rightarrow 24{r^2} - 84r + 36 = 0 \\
  {\text{On dividing the equation by 6}} \\
   \Rightarrow {\text{4}}{{\text{r}}^2} - 14r + 6 = 0 \\
  {\text{on dividing the equation by 2}} \\
   \Rightarrow {\text{2}}{{\text{r}}^2} - 7r + 3 = 0 \\
\]
This is the final equation, now get the value of r
using the formula
\[
  \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} \\
  a = 2 \\
  b = - 7 \\
  c = 3 \\
  \dfrac{{ + 7 \pm \sqrt {{7^2} - 4 \times 2 \times 3} }}{{2 \times 2}} \\
   \Rightarrow \dfrac{{ + 7 \pm \sqrt {49 - 24} }}{4} \\
   \Rightarrow \dfrac{{7 \pm \sqrt {25} }}{4} \\
   \Rightarrow \dfrac{{7 \pm 5}}{4} \\
   \Rightarrow {r_1} = \dfrac{{7 + 5}}{4} = \dfrac{{12}}{4} = 3 \\
   \Rightarrow {r_2} = \dfrac{{7 - 5}}{4} = \dfrac{2}{4} = \dfrac{1}{2} \\
\] $r = 3$
Now put the values $r = 3,\dfrac{1}{2},0$ as the value of $x,y$ in given equation
\[
  4x + 3y - 6 = 0 \\
  {\text{put r}} = 3 \\
  4 \times 3 + 3 \times 3 - 6 = 12 + 9 - 6 = 15 \\
  {\text{put r}} = \dfrac{1}{2} \\
  4x + 3y - 6 = 0 \\
  4 \times \dfrac{1}{2} + 3 \times \dfrac{1}{2} - 6 = 2 + 1.5 - 6 = - 2.5 \\
  {\text{put r}} = 0 \\
  4x + 3y - 6 = 0 \\
  4 \times 0 + 3 \times 0 - 6 = - 6 \\
\]
Only gives positive result rest are negative terms so ignore them
Put $r = 3$ in circle equation
\[
  {\left( {x - \dfrac{1}{2}} \right)^2} + {\left( {y - \dfrac{1}{2}} \right)^2} = \dfrac{1}{4} \\
   \Rightarrow {x^2} + \dfrac{1}{4} - x + {y^2} + \dfrac{1}{4} - y = \dfrac{1}{4} \\
   \Rightarrow \left( {{x^2} + {y^2} - x - y} \right) + 2/4 = \dfrac{1}{4} \\
   \Rightarrow 4\left( {{x^2} + {y^2} - x - y} \right) + 1=0 \\
\]
This is our answer
Hence Option B is the right answer.

Note: First we have calculated all the coordinate axes of \[x,y\], then put these values in the original equation then find the coordinates of centre r , after that calculate all the values of r by using the formula. And finally put these values in the equation of the circle. Hence we get our answer.