Question

The equation of a straight line which cuts off an intercept of 5 units on the negative direction of the y-axis and makes an angle of \[120{}^\circ \] with the positive x-axis is
 (A) \[y+\sqrt{3}x+5=0\]
(B) \[y-\sqrt{3}x+5=0\]
(C) \[y+\sqrt{3}x-5=0\]
(D) \[y-\sqrt{3}x-5=0\]

Answer 1

Hint: The length of the intercept made by the straight line on the negative y-axis is 5 units and the measure of the angle made by the straight line with the positive x-axis is equal to \[120{}^\circ \]. Since the y-intercept of the line is with the negative y-axis, so the y-intercept must be equal to -5. We know the property that the slope of a straight line is equal to the tangent of the angle made by the straight line with the positive x-axis. Now, get the slope and intercept of the straight line. The standard equation of the straight line, \[y=mx+c\] where \[m\] is the slope and \[c\] is the y-intercept of the straight line. Now, solve it further and get the slope of the straight line.

Complete step-by-step solution:
According to the question, we are given that a straight line cuts off an intercept of 5 units on the negative direction of the y-axis and makes an angle of \[120{}^\circ \] with the positive x-axis.
The length of intercept made by the straight line on negative y-axis = 5 units …………………………………………….(1)
The measure of the angle made by the straight line with the positive x-axis = \[120{}^\circ \]……………………………………………(2)
We know the standard equation of the straight line, \[y=mx+c\] where \[m\] is the slope and \[c\] is the y-intercept of the straight line ……………………………………..(3)
Here, in the question, we are asked to find the equation of the straight line and for the equation of a straight line, we need the slope and y-intercept of the straight line.
From equation (1), we have the length of y-intercept with the negative y-axis. Since the y-intercept of the line is with the negative y-axis, so the y-intercept must be equal to -5.
The y-intercept of the straight line = -5 ……………………………………………..(4)
From equation (2), we have the angle made by the straight line with the positive x-axis.
We know the property that the slope of a straight line is equal to the tangent of the angle made by the straight line with the positive x-axis.
Using the above property, we get
The slope of the straight line = \[\tan \left( 120{}^\circ \right)=\tan \left( 180{}^\circ -60{}^\circ \right)\] ………………………………………(5)
We know the property that \[\tan \left( 180{}^\circ -\theta \right)=-\tan \theta \] ………………………………………(6)
We also know that \[\tan \left( 60{}^\circ \right)=\sqrt{3}\] ………………………………………….(7)
Now, from equation (5), equation (6), and equation (7), we get
The slope of the straight line = \[\tan \left( 120{}^\circ \right)=\tan \left( 180{}^\circ -60{}^\circ \right)=-\tan 60{}^\circ =-\sqrt{3}\] ……………………………………….(8)
Now, from equation (2), equation (4), and equation (8), we get
The equation of the given straight line,
\[\Rightarrow y=-\sqrt{3}x-5\]
\[\Rightarrow y+\sqrt{3}x+5=0\] ……………………………………(9)
Therefore, the equation of the straight line is \[y+\sqrt{3}x+5=0\] .

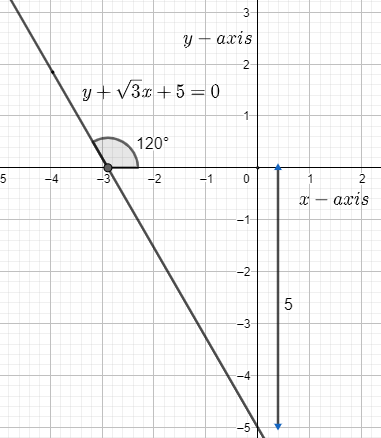
Hence, the correct option is (A).

Note: In this question, one might make a silly mistake and take the y-intercept equal to 5 units. This is wrong. Since the straight line is cutting 5 units with the negative y-axis, so the y-intercept of the given straight line is equal to -5 units.