Question

The equation of a stationary wave is $y = sin\left(\dfrac{\pi}{3}x\right)cos(10\pi t)$, where x and y are in cm. What is the distance between adjacent nodes?
A. 2 cm
B. 3 cm
C. 6 cm
D. 4 cm

Answer 1

Hint: Compare the given equation with the standard stationary wave equation and deduce what the value of the propagation constant is. Using the relation between the propagation constant and wavelength over an entire cycle of vibration, determine the wavelength of the vibration. Now, using the fact that the distance between adjacent nodes is half the wavelength of a vibration, numerically arrive at the appropriate solution.

Formula used:
propagation constant $k =\dfrac{2\pi}{\lambda}$
Distance between adjacent nodes: $d =\dfrac{\lambda}{2}$

Complete answer:
Let us begin by understanding what stationary waves are.
Stationary waves, also known as standing waves, are formed as a result of an interference of two progressive waves of the same type, same amplitude and same frequency, travelling in opposite directions along the same line of propagation.
Due to this stationary wave formation, particles at some points of the medium do not vibrate at all. These points of zero amplitude are called nodes. However, particles at some other points of the medium vibrate with maximum amplitude. These points of maximum amplitude are called antinodes.

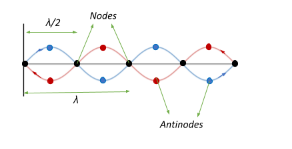
In a stationary wave, the distance between two successive nodes (or antinodes) is $\lambda/2$, where $\lambda$ is the wavelength of the wave.
Now, the general form of a stationary wave equation is:
$y = asin(kx)cos(\omega t)$, where a is the amplitude of vibration, k is the propagation constant, $\omega$ is the angular frequency and t is the instantaneous time.
The given stationary wave equation is:
$y = sin\left(\dfrac{\pi}{3}x\right)cos(10\pi t)$
Comparing the two equations, we see that $k = \dfrac{\pi}{3}$.
The propagation constant k is generally expressed in terms of wavelength as: $k = \dfrac{2\pi}{\lambda}$
Equating the two, we get:
$\dfrac{\pi}{3} = \dfrac{2\pi}{\lambda} \Rightarrow \lambda = 6\;cm$
The distance between consecutive nodes is thus, $\dfrac{\lambda}{2} = \dfrac{6}{2} = 3\;cm$

So, the correct answer is “Option B”.

Note:
Always remember that for a standing wave, the nodes and antinodes are alternately produced with a distance between a node and an antinode being $\lambda/4$, and the distance between two successive nodes (or antinodes) is $\lambda/2$.