Question

The equation of a parabola is ${{\left( x-2 \right)}^{2}}=3\left( y+1 \right)$. S is the focus and Z is the foot of the perpendicular drawn from S to the directrix of the parabola. Find the midpoint of SZ.
A. $\left( -2,1 \right)$
B. $\left( 2,-1 \right)$
C. $\left( 2,1 \right)$
D. $\left( -2,-1 \right)$

Answer 1

Hint: The equation of the parabola is given. From the equation, we try to find out the coordinates of the focus and equation of the directrix. We try to establish the relation between the perpendicular od the axis and the directrix. We find the foot of the perpendicular from the focus using the previous relation. After getting that point, we use the focus point to find out the middle point.

Complete step-by-step solution:
The equation of a parabola is ${{\left( x-2 \right)}^{2}}=3\left( y+1 \right)$. So, it is of the general form ${{\left( x-m \right)}^{2}}=4a\left( y-n \right)$ where the vertex is $\left( m,n \right)$. The length of latus rectum is 4a.
Focus is $\left( m,n+a \right)$. Equation of directrix is $y=n-a$. The distance between the focus and the directrix is 2a.
Now, we try to equate the general equation with the given equation.
So, equating we get the vertex is $\left( 2,-1 \right)$. The length of the latus rectum is 3.
So, the value of a is $\dfrac{3}{4}$.
Focus is $S\equiv \left( 2,-1+\dfrac{3}{4} \right)\equiv \left( 2,-\dfrac{1}{4} \right)$. Equation of directrix is $y=-1-\dfrac{3}{4}=-\dfrac{7}{4}$. The distance between the focus and the directrix is $\dfrac{3}{2}$.

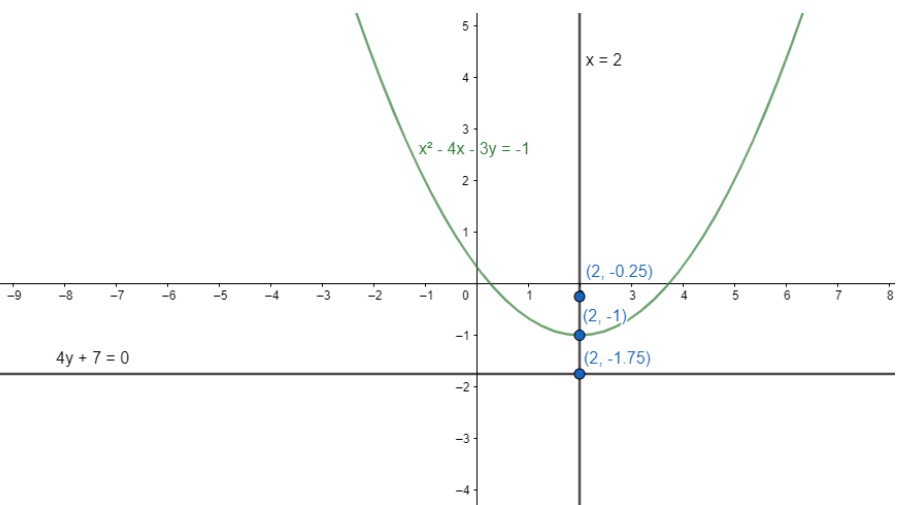
Now we know that the directrix and the axis of a parabola is always perpendicular to each other.
So, the foot of the perpendicular drawn from the focus to the directrix of the parabola will be on the axis and directrix both.
The foot will be the intersecting point of the directrix and the axis of the parabola.
The coordinate of the foot will be $\left( m,n-a \right)$.
In this particular parabolic equation, the point is $\left( 2,-1-\dfrac{3}{4} \right)\equiv \left( 2,-\dfrac{7}{4} \right)$.
So, $S\equiv \left( 2,-\dfrac{1}{4} \right)$ and $Z\equiv \left( 2,-\dfrac{7}{4} \right)$
Middle point of two points $\left( u,v \right)$ and $\left( w,x \right)$ will be $\left( \dfrac{u+w}{2},\dfrac{v+x}{2} \right)$.
Now, we find the middle point of SZ.
The middle point is $\left( \dfrac{2+2}{2},\dfrac{-\dfrac{1}{4}-\dfrac{7}{4}}{2} \right)\equiv \left( 2,-1 \right)$.

Note: Although we calculated the whole problem, we can use one more trick to find the answer without calculating anything. We have to remember that the vertex is always equidistant from both the focus and the directrix. So, the midpoint of the focus and the foot of the perpendicular drawn from the focus to the directrix of the parabola is the vertex itself. That’s why we got back the coordinate of the vertex $\left( 2,-1 \right)$ as the solution.