Question

the equation of a circle is ${x^2} + {y^2} = 25$, the equation of its chord whose middle points (1,-2) is given by:
(A) $x + 2y - 5 = 0$
(B) $x + 2y + 5 = 0$
(C) $x - 2y - 5 = 0$
(D) $2x + y - 5 = 0$

Answer 1

Hint: In the question we have given the equation of the circle and middle point of the circle. So we draw a circle and calculate the slope of the equation and then find the required equation.

Complete step-by-step answer:

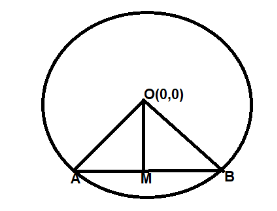
We have given an equation of circle in the question
 i.e. ${x^2} + {y^2} = 25$ (1)
And we know that the question of circle is ${x^2} + {y^2} = {a^2}$ (2)
Where a is radius of the circle and the center of the circle is $\left( {0,0} \right)$and here M is the midpoint of AB
And now we find the value of radius by equating the equation (1) and (2)
$
  {a^2} = 25 \\
   \Rightarrow a = \sqrt {25} \\
   \Rightarrow a = 5 \\
 $
Now with the help of diagram $OM \bot AB$, And we know the property of perpendicular i.e.
${m_{OM}} \times {m_{AB}} = - 1$ (3)
We know the slope of median is
$ \Rightarrow {m_{om}} = \left( {\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}} \right)$
Now we put the value of (x, y) in the equation we get,
$
   \Rightarrow {m_{om}} = \left( {\dfrac{{0 - \left( { - 2} \right)}}{{0 - 1}}} \right) \\
   \Rightarrow {m_{om}} = - 2 \\
 $
So put the value of ${m_{om}}$ in equation (3), we get
$
   - 2 \times {m_{AB}} = - 1 \\
   \Rightarrow {m_{AB}} = \dfrac{1}{2} \\
 $
This means M is lies on AB
Now we are using the formula of middle point as
$\left( {{y_2} - {y_1}} \right) = m\left( {{x_2} - {x_1}} \right)$
So we have point $\left( {{\text{1, - 2}}} \right){\text{ and }}{{\text{m}}_{{\text{ab}}}}{\text{ = }}\dfrac{{\text{1}}}{{\text{2}}}$ and put these values in the formula we get
\[ \Rightarrow y - \left( { - 2} \right) = \dfrac{1}{2}\left( {x - 1} \right)\]
We solve the brackets we get
\[ \Rightarrow y + 2 = \dfrac{{x - 1}}{2}\]
Now as 2 in the denominator of R.H.S we take it to the L.H.S it get multiplied with the term, we get
\[ \Rightarrow 2\left( {y + 2} \right) = x - 1\]
\[ \Rightarrow 2y + 4 = 4 + 1\]
After solving the equation we get
\[
   \Rightarrow x - 2y = 5 \\
   \Rightarrow x - 2y - 5 = 0 \\
 \]
So, the required equation is $x - 2y - 5 = 0$.

Hence option C is correct.

Note: Here one triangle is formed one terminal of triangle at center of circle and middle of one side is given form that we will applying formula of midpoint we will find another two terminal and radius is given that by that we will apply distance formula and distance is radius, by this we will get to know all three terminal of triangle and triangle lower side we can find that by help of these terminals and lower side is equal to chord of circle.