Question

The equation of a circle in parametric form is given by \[x = a\cos \theta ,y = a\sin \theta \], if the tangents from P(h,k) to the circle intersects it at Q and R, then the equation of the circle circumscribed of \[\Delta PQR\] is?

Answer 1

Hint: The given question is about solving for the equation of the circle, which is inscribed in the triangle, and has an intersection at the given points. Here we are given with the parametric coordinates, and to solve further we need to square and add both the coordinates.
Formulae Used: Equation of circle between two points says A(a,b) B(c,d); (point A is centre of circle and B is a point outside the circle)
\[ \Rightarrow (x - a)(x - c) + (y - b)(y - kd) = 0\]

Complete step-by-step solution:
The given question needs to obtain the equation of the circle, and the parametric coordinates are given, on solving we get:
Given,
\[ \Rightarrow x = a\cos \theta ,y = a\sin \theta \]
Now we have to square and add the given coordinates:
\[
   \Rightarrow x = a\cos \theta ,y = a\sin \theta \\
   \Rightarrow {x^2} + {y^2} = {(a\cos \theta )^2} + {(a\sin \theta )^2} \\
   \Rightarrow {x^2} + {y^2} = {a^2}({\cos ^2}\theta + {\sin ^2}\theta ) \\
   \Rightarrow {x^2} + {y^2} = {a^2}[({\cos ^2}\theta + {\sin ^2}\theta = 1)] \\
 \]
Here we get the centre of the circle as (0,0)

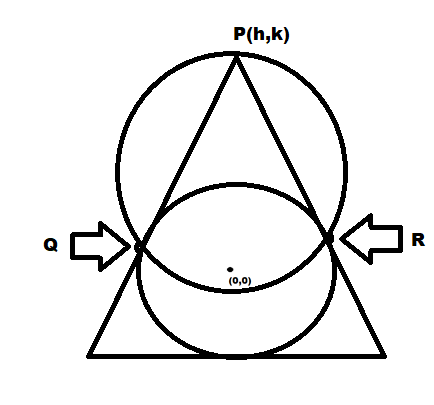
Here in the above figure:
\[ \Rightarrow \sin ce,\angle OQP = \angle QRP = \dfrac{\pi }{2}\]
The circle on OP as diameter is the circumscribed of \[\Delta PQR\]
Equation of circle between two points says A(a,b) B(c,d); (point A is centre of circle and B is a point outside the circle)
\[ \Rightarrow (x - a)(x - c) + (y - b)(y - kd) = 0\]
Here for our question the two points are: (0,0) and (h,k)
Therefore, its equation will be:
\[
   \Rightarrow (x - 0)(x - h) + (y - 0)(y - k) = 0 \\
   \Rightarrow {x^2} + {y^2} - hx - ky = 0 \\
 \]
This is the required equation of the circle.

Note: The given question is of coordinate geometry in which we need to obtain the equation of the circle, which is circumscribed under the triangle, and here to solve this question we need to make a general equation of the circle and then put the values given to obtain the equation.