Question

The equation ${{\left| z-1 \right|}^{2}}+{{\left| z+1 \right|}^{2}}=2$ represents
[a] A circle of radius 1
[b] A straight line
[c] An ordered pair (0,0)
[d] A set of two points.

Answer 1

Hint: Assume that the point z on the curve be given by x+iy. Use the fact that if z = x+iy, then $\left| z \right|=\sqrt{{{x}^{2}}+{{y}^{2}}}$. Hence find the value of ${{\left| z-1 \right|}^{2}}+{{\left| z+1 \right|}^{2}}$ and hence find the cartesian form of the curve ${{\left| z-1 \right|}^{2}}+{{\left| z+1 \right|}^{2}}=2$. Hence find the nature of the curve represented by the equation ${{\left| z-1 \right|}^{2}}+{{\left| z+1 \right|}^{2}}=2$.

Complete step by step solution:
Let z = x+iy be a general point on the curve ${{\left| z-1 \right|}^{2}}+{{\left| z+1 \right|}^{2}}=2$
Now, we have
$\left| z-1 \right|=\left| x+iy-1 \right|=\left| \left( x-1 \right)+iy \right|$
We know that if z = x+iy, then $\left| z \right|=\sqrt{{{x}^{2}}+{{y}^{2}}}$.
Hence, we have
$\left| z-1 \right|=\sqrt{{{\left( x-1 \right)}^{2}}+{{y}^{2}}}$
Squaring both sides, we get
${{\left| z-1 \right|}^{2}}={{\left( x-1 \right)}^{2}}+{{y}^{2}}$
Also, we have
$\left| z+1 \right|=\left| x+iy+1 \right|=\left| \left( x+1 \right)+iy \right|$
We know that if z = x+iy, then $\left| z \right|=\sqrt{{{x}^{2}}+{{y}^{2}}}$.
Hence, we have
$\left| z+1 \right|=\sqrt{{{\left( x+1 \right)}^{2}}+{{y}^{2}}}$
Squaring both sides, we get
${{\left| z+1 \right|}^{2}}={{\left( x+1 \right)}^{2}}+{{y}^{2}}$
Hence, we have
${{\left| z-1 \right|}^{2}}+{{\left| z+1 \right|}^{2}}={{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( x+1 \right)}^{2}}+{{y}^{2}}$
We know that ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$ and ${{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$
Hence, we have
${{\left| z-1 \right|}^{2}}+{{\left| z+1 \right|}^{2}}={{x}^{2}}-2x+1+{{y}^{2}}+{{x}^{2}}+2x+1+{{y}^{2}}$
Simplifying, we get
${{\left| z-1 \right|}^{2}}+{{\left| z+1 \right|}^{2}}=2\left( {{x}^{2}}+{{y}^{2}}+1 \right)$
Hence, we have
$\begin{align}
  & {{\left| z-1 \right|}^{2}}+{{\left| z+1 \right|}^{2}}=2 \\
 & \Rightarrow 2\left( {{x}^{2}}+{{y}^{2}}+1 \right)=2 \\
\end{align}$
Dividing both sides by 2, we get
${{x}^{2}}+{{y}^{2}}+1=1$
Subtracting 1 from both sides, we get
${{x}^{2}}+{{y}^{2}}=0$
Since ${{x}^{2}}\ge 0,{{y}^{2}}\ge 0\forall x,y\in \mathbb{R}$, we have
$\forall x,y\in \mathbb{R},{{x}^{2}}+{{y}^{2}}\ge 0$ with equality when x = 0, y = 0
Hence, we have
$x=0,y=0$ is the only point satisfying the equation.
Hence equation ${{\left| z-1 \right|}^{2}}+{{\left| z+1 \right|}^{2}}=2$ represents the point (0,0) in the argand plane.
Hence option [c] is correct.
Note: Alternative solution:
We know that $\left| z-{{z}_{0}} \right|$ represents the distance of point $z$ from point ${{z}_{0}}$ in the argand plane.
Hence, $\left| z-1 \right|$ represents the distance of point z from point $1+0i$ in argand plane.
Similar $\left| z+1 \right|$ represents the distance of point z from point $-1+0i$
The point $x+iy$ is represented by $\left( x,y \right)$ ordered pair in the argand plane.
Hence 1+0i will be represented by the ordered pair B (1,0) as shown in the diagram below and |z-1| will be the distance PB of point P(z) from B.
Similarly -1+0i will be represented by the ordered pair A (-1,0) as shown in the diagram below and |z+1| will be the distance PA of point P(z) from B.

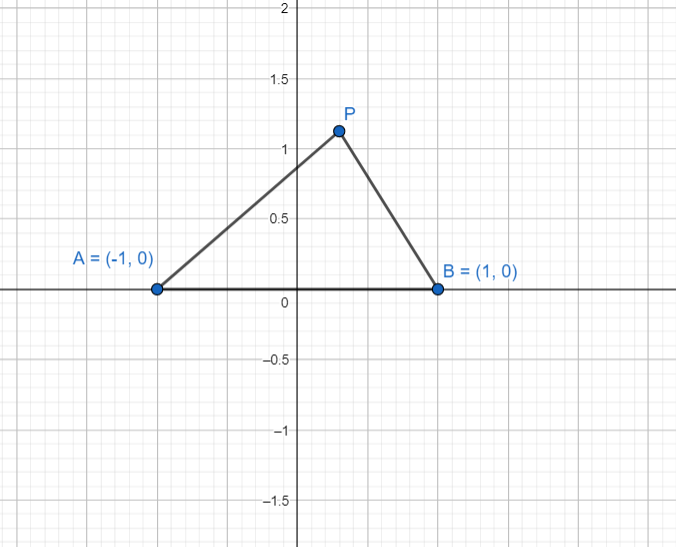
Let P(z) be any point on the curve ${{\left| z-1 \right|}^{2}}+{{\left| z+1 \right|}^{2}}=2$
Hence, we have
$P{{A}^{2}}+P{{B}^{2}}=2$
We know that $AM\ge GM$
Hence, we have
$\begin{align}
  & \dfrac{P{{A}^{2}}+P{{B}^{2}}}{2}\ge \sqrt{P{{A}^{2}}P{{B}^{2}}} \\
 & \Rightarrow PAPB\le 1 \\
\end{align}$
Equality at PA = PB.
Now in triangle PAB, we have
$\cos P=\dfrac{P{{A}^{2}}+P{{B}^{2}}-A{{B}^{2}}}{2PAPB}=\dfrac{2-{{2}^{2}}}{2PAPB}=\dfrac{-1}{PAPB}$
Since $PAPB\le 1\Rightarrow \dfrac{1}{PAPB}\ge 1$
Hence, we have
$\dfrac{-1}{PAPB}\le -1$
Hence, we have
$\cos P\le -1$
But $\cos P\ge -1$
Hence, we have
$\cos P=-1$
Hence, $P=\pi $
In other words A, P and B are collinear.
and PAPB = 1
But since equality occurs only when PA = PB.
Hence, we have PA = PB and A, P and B are collinear.
Hence by midpoint theorem, we have
$P\equiv \left( \dfrac{-1+1}{2},\dfrac{0+0}{2} \right)=\left( 0,0 \right)$
Hence option [c] is correct