Question

The equation ax + by + c = 0 represents a straight line
(a) For all real numbers a, b and c
(b) \[\text{Only when }a\ne 0\]
(c) \[\text{Only when b}\ne 0\]
(d) Only when at least one of a and b is non – zero

Answer 1

Hint:To solve this question, we will assume different values of a, b and c and then we will check at what values of a, b and c, we will get a line and what values, we will get some other things like points, etc. On the basis of this, we will select the appropriate option.

Complete step-by-step answer:
Before we solve this question, we must know what a straight line is. A straight line is formed when the points are joined continuously such that any three points will be collinear or the area between them will be zero. Now, we are going to consider different cases based on different values of a, b and c. So, we have the following cases.
Case 1: The values of a, b and c are non – zero. Thus, the equation of line we will get is: ax + by + c = 0. Now, this is the general equation of the line which is as shown:

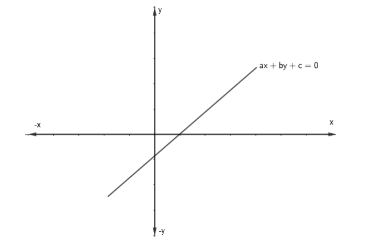
So, in this case, we will obtain a line. The slope may be different on the basis of the values of a, b and c.

Case 2: The values of a, b, and c are zero. In this case, the equation we will get is: (0)x + (0)y + (0) = 0. This equation satisfies no matter what the values of a, b, and c are. Thus, in this case, instead of a line, we will get an entire x – y plane.

Case 3: Either a or b is non – zero. If a = 0, then the equation of the line will be by + c = 0. We will obtain a line parallel to the x axis. If b = 0, then the equation of the line will be ax + c = 0. We will obtain a line parallel to the y-axis.
 

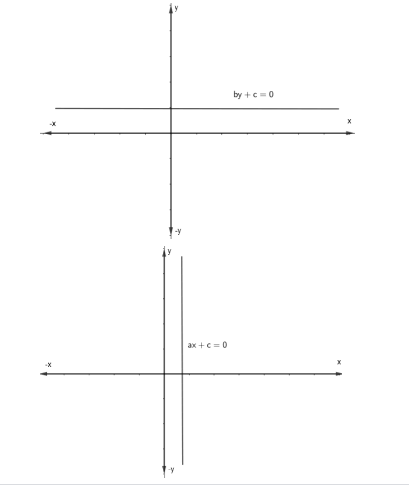
Hence, for the line to exist, at least one of a and b is non – zero.
Therefore, option (d) is the right answer.

Note: We can also have the following situation. Both a and b are zero and c is a non – zero real number. The equation we will get in this case is 0 + 0 + c = 0. So, c = 0. But we have assumed that c is a non – zero non-real number, so we will get nothing in this case. This is the reason that option (a) is not correct because when a = 0, b = 0, and \[c=\alpha \] (non – zero), we will not get a line.