
The equation \[4x + 7 = 2x + 9\;\] is modelled as shown in the figure.
Which value of \[x\] would make the equation true?
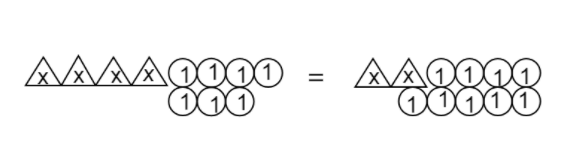
A. 1
B. 2
C. 8
D. 16
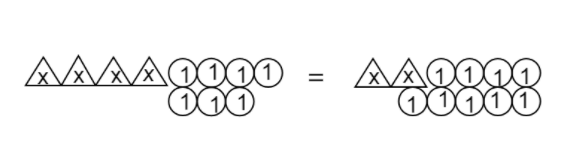
Answer
478.2k+ views
Hint:In the above given question, we are given a model of the equation \[4x + 7 = 2x + 9\;\] . The model is shown with the help of triangles and circles. Here, the variable \[x\] is represented by showing it under the triangles and the constant is represented by showing it with a number of circles next to the triangles. We have to find the value of \[x\] for which the given equation of \[x\] becomes true. In order to approach the solution, we can use the given model of the equation.
Complete step by step answer:
Given that, a pair of linear equations which are equal to each other and they are given by the combined equation which is written as,
\[ \Rightarrow 4x + 7 = 2x + 9\;\]
We have to find the value of \[x\] using the above given model of the equation which satisfies the above given equation.
Consider the LHS of the equation which is \[4x + 7\;\] .Here the variable part is represented by four triangles and the constant is represented by seven circles.Similarly, in the RHS of the above equation i.e. \[2x + 9\;\]. The variable part is represented by two triangles and the constant is represented by nine circles.Now, to solve this equation, we can cancel the equal number of triangles and circles present in the LHS and in the RHS.Therefore, the two triangles of RHS will cancel the two in the LHS and similarly the seven circles of the LHS will cancel the seven circles of the RHS.
Now only two triangles and two circles are remaining in the model of the given equation.
That gives us the new model as,
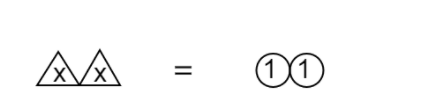
Therefore, that means the two triangles of variable \[x\] are equal to the two circles of the constant \[1\]. Hence, each triangle of variable \[x\] is equal to a circle of constant \[1\]. That gives us the final model as,
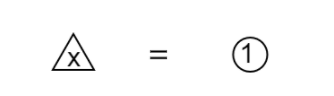
Hence the variable \[x\] is equal to the constant \[1\] i.e.
\[ \Rightarrow x = 1\]
Hence, the value \[x = 1\] will make the equation \[4x + 7 = 2x + 9\;\] true.
So the correct option is A.
Note:Alternatively, we can also solve the above given equation by using another method to find the value of the variable \[x\] in a quicker and convenient way.
Since the given equation of \[x\] is written as,
\[ \Rightarrow 4x + 7 = 2x + 9\;\]
Now, transfer the constant \[7\] to the RHS and the variable \[2x\] to the LHS.
That gives us the equation as,
\[ \Rightarrow 4x - 2x = 9\; - 7\]
\[ \Rightarrow 2x = 2\]
Dividing both sides by \[2\] we get,
\[ \Rightarrow x = 1\]
Therefore the value of the variable \[x\] which can satisfy the given equation is \[1\].
Complete step by step answer:
Given that, a pair of linear equations which are equal to each other and they are given by the combined equation which is written as,
\[ \Rightarrow 4x + 7 = 2x + 9\;\]
We have to find the value of \[x\] using the above given model of the equation which satisfies the above given equation.
Consider the LHS of the equation which is \[4x + 7\;\] .Here the variable part is represented by four triangles and the constant is represented by seven circles.Similarly, in the RHS of the above equation i.e. \[2x + 9\;\]. The variable part is represented by two triangles and the constant is represented by nine circles.Now, to solve this equation, we can cancel the equal number of triangles and circles present in the LHS and in the RHS.Therefore, the two triangles of RHS will cancel the two in the LHS and similarly the seven circles of the LHS will cancel the seven circles of the RHS.
Now only two triangles and two circles are remaining in the model of the given equation.
That gives us the new model as,
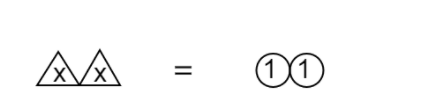
Therefore, that means the two triangles of variable \[x\] are equal to the two circles of the constant \[1\]. Hence, each triangle of variable \[x\] is equal to a circle of constant \[1\]. That gives us the final model as,
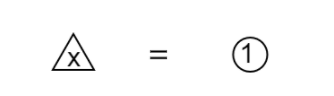
Hence the variable \[x\] is equal to the constant \[1\] i.e.
\[ \Rightarrow x = 1\]
Hence, the value \[x = 1\] will make the equation \[4x + 7 = 2x + 9\;\] true.
So the correct option is A.
Note:Alternatively, we can also solve the above given equation by using another method to find the value of the variable \[x\] in a quicker and convenient way.
Since the given equation of \[x\] is written as,
\[ \Rightarrow 4x + 7 = 2x + 9\;\]
Now, transfer the constant \[7\] to the RHS and the variable \[2x\] to the LHS.
That gives us the equation as,
\[ \Rightarrow 4x - 2x = 9\; - 7\]
\[ \Rightarrow 2x = 2\]
Dividing both sides by \[2\] we get,
\[ \Rightarrow x = 1\]
Therefore the value of the variable \[x\] which can satisfy the given equation is \[1\].
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE





